1. INTRODUCTION
Bamboo is a highly versatile and sustainable material that has been utilized for centuries in various human activities. It is particularly valued for its rapid growth and short maturation cycle of 3–5 years (Eratodi, 2017). In recent years, modern bamboo construction has garnered increasing global interest, with notable examples including the Sharma Springs openwork bamboo house in Bali, Indonesia; the bamboo pedestrian bridge in Matina Municipality, Davao, Philippines; the Crosswaters Ecolodge bamboo bridge in China; and bamboo mattresses used to enhance soil bearing capacity in Jombang and Madiun, East Java, Indonesia (Fitrianto, 2015; Lapina and Zakieva, 2021; Medina Yor Maikol et al., 2020; Ready et al., 2020). Bamboo can serve both non-structural and structural functions, highlighting the importance of understanding its physical and mechanical characteristics in structural applications. Numerous experimental studies have investigated its tensile, compressive, and flexural performance, as summarized in Tables 1–3.
| Previous research | Bamboo species | Tensile properties | |
|---|---|---|---|
| Strength | Modulus of elasticity | ||
| (MPa) | (MPa) | ||
| Gunawan et al. (2015) | Dendrocalamus asper with node (top part) | 197.28* | 4,320 |
| D. asper with node (middle part) | 243.81* | 3,128 | |
| D. asper with node (bottom part) | 169.03* | 1,810 | |
| D. asper without node (top part) | 313.93* | 5,916 | |
| D. asper without node (middle part) | 260.37* | 5,505 | |
| D. asper without node (bottom part) | 250.21* | 2,139.67 | |
| Widoyoko (2018) | Wulung bamboo without node | 250.14* | 23,240 |
| Gauss et al. (2019) | Brazilian Phyllostachys edulis bamboo with a node | 100* | 11,190 |
| Brazilian P. edulis bamboo without nodes | 275* | 17,740 | |
| Lubis (2019) | Wulung bamboo with a node | 92.40* | 13,222 |
| Wulung bamboo without nodes | 195.30* | 18,576 | |
| De Jesus et al. (2021) | D. asper | 242.75–470.06 | - |
| D. asper | 168.80–356.93 | - | |
| Cai et al. (2023) | Moso bamboo with a node | 103.91–120.34 | 8,472–9,101 |
| Moso bamboo without nodes | 177.80–189.76 | 7,475–8,216 | |
| Meng et al. (2023) | Moso bamboo with a node | 73.66–85.74 | - |
| Moso bamboo without nodes | 134.83–76.66 | - | |
| Li et al. (2024) | Laminated Moso bamboo | 77.18* | 7,777 |
| Previous research | Bamboo species | Compressive properties | |
|---|---|---|---|
| Strength | Modulus of elasticity | ||
| (MPa) | (MPa) | ||
| Hoque et al. (2019) | Bangladeshi green bamboo with a node | 26.3–54.18 | 2,300–8,500 |
| Bangladeshi green bamboo without nodes | 18.93–23 | 300–1,100 | |
| Gauss et al. (2019) | Brazilian Phyllostachys edulis bamboo with a node | 59.5* | 20,640* |
| Brazilian P. edulis bamboo without nodes | 57.5* | 20,380* | |
| Lubis (2019) | Wulung bamboo with a node | 53.44* | 15,482* |
| Wulung bamboo without nodes | 56.37* | 13,891* | |
| De Jesus et al. (2021) | D. asper with node | 44.83–63.21 | - |
| D. asper without node node | 43.83–69.60 | - | |
| Liu et al. (2021) | Moso bamboo with a node | 59.80* | - |
| Moso bamboo without nodes | 57.20* | - | |
| Hartono et al. (2022) | D. asper | 41–50 | - |
| Meng et al. (2023) | Moso bamboo with a node | 32.03–48 | - |
| Moso bamboo without nodes | 30.07–47.71 | - | |
| Li et al. (2024) | Laminated Moso bamboo | 59.74* | 9,777* |
| Previous research | Brief description |
|---|---|
| Kim et al. (2018) | A study was conducted to evaluate the effect of span length on the bending properties of larch lumber. Two types of specimens were used, with lengths of 1,650 mm and 3,000 mm. The observed parameters included bending strength and modulus of elasticity. |
| Lee et al. (2018) | The longitudinal bond strength of larch wood was assessed through experimental testing. Six types of end-joint specimens were examined, with each joint located at the mid-span of the beam. Observations included failure modes, load–deflection responses, and calculations of flexural strength and modulus of elasticity. |
| Maulana et al. (2019) | Static and dynamic bending tests were performed on oriented strand boards (OSBs) made from Dendrocalamus asper under various shelling ratios. The evaluated properties included static bending strength, static modulus of elasticity (MOE), and dynamic modulus of elasticity. The correlation between static and dynamic MOE was also examined. |
| Galih et al. (2020) | Bending tests were conducted to evaluate the mechanical performance of tropical hybrid cross-laminated timber (CLT). The core layer consisted of bamboo laminated board made from P. edulis, while the face layers were composed of rubberwood (Hevea brasiliensis) and jelutong (Dyera costulata). The primary properties investigated were bending strength and modulus of elasticity. |
| Iswanto et al. (2020) | Sandwich particleboards were investigated for their potential application as building acoustic materials. The boards were fabricated using Gigantochloa pruriens and Gigantochloa apus. In this study, the bending strength and modulus of elasticity were evaluated. |
| Deng and Peng (2021) | An experimental study was conducted to investigate the bending properties of Moso bamboo (P. edulis). The data collected included load–deflection and load–strain curves, bending strength, and elastic modulus. However, the position of the neutral axis was not addressed in the study. |
| Wang et al. (2023) | Experimental and numerical studies were carried out to investigate the effect of nodes on the flexural behavior of Moso bamboo (P. edulis). The comparison focused on the load–deflection curves obtained from both the experimental tests and finite element analysis. In the experimental study, strain measurements were not conducted; only the load–deflection response was recorded. |
| Zhang et al. (2024) | The effect of load duration on the flexural strength of InorgBam was evaluated under long-term loading conditions. The specimens were fabricated using Moso bamboo (P. edulis) and bonded with magnesium oxysulfide adhesive. The experimental results captured the relationship between flexural strength and load duration. |
| Li et al. (2024) | An experimental study was conducted on I-shaped laminated bamboo members. The investigation included observations of failure modes, strain distribution, load–deflection behavior, elastic proportional limit, ultimate limit, and failure limit. However, tensile and compressive tests parallel to the grain were not performed, which prevented a detailed analysis of stress distribution. |
| Rofii et al. (2024) | The bending properties of laminated boards made from Petung bamboo (D. asper) were investigated. Flexural tests were conducted to determine the bending strength and modulus of elasticity. |
| Sumardi et al. (2022) | Experimental studies were conducted on bamboo zephyr composites made from G. apus and falcata veneer. The objective of the study was to determine the bending strength and modulus of elasticity. |
| Awaludin et al. (2025) | The flexural properties of glulam beams made from various wood species—including Jabon, Pine, Mahogany, Mangium, Rubberwood, Merbau, Keruing, Meranti Batu, and Bangkirai—were investigated. The experimental results included load–deflection curves, bending strength, and modulus of elasticity. |
Tables 1 and 2 show that bamboo exhibits different mechanical properties in tension and compression parallel to the grain. Theoretically, these differences cause the neutral axis in bamboo culm beams to shift away from the centroidal axis (Tian et al., 2021). However, a review of Tables 1–3 reveals a lack of comprehensive experimental studies that investigate the interrelation of tensile and compressive strengths parallel to the grain with flexural behavior, particularly concerning the determination of the neutral axis position and prediction of the normal stress distribution across the cross-section. Gauss et al. (2019) observed the neutral axis of bamboo split under flexural loads, but not specifically in culm-shaped bamboo beams. Additionally, Li et al. (2024) observed strain distribution across the entire section of I-shaped laminated bamboo, enabling identification of the neutral axis location.
Bamboo is considered a linear and homogeneous material in the design of bamboo beam structures. In addition, the tensile modulus of elasticity is assumed to be the same as the compressive modulus of elasticity (International Organization for Standardization, 2021b). Therefore, in the calculation of bamboo beam design, the neutral axis is located at 1/2 the diameter of the bamboo. For design purposes, this assumption may be sufficient. However, along with the development of science, a study of the behavior of bamboo beams that considers mechanical properties closer to reality is needed. Therefore, this study aims to experimentally investigate the position of the neutral line in bamboo beams. The bamboo used in this study is Wulung bamboo (Gigantochloa atroviolacea), which is commonly used for building structures in Indonesia (Irnawan, 2022).
Tensile, compression, and bending tests were performed according to ISO 22157:2019. The results of the will provide comprehensive information about the load–deflection curve, strain distribution in the cross-section of the bamboo beam at mid-span, neutral axis position in the cross-section of the bamboo beam at mid-span, modulus of rupture, tensile strength, compressive strength, and flexural, tensile, and compressive elastic moduli. These findings will be valuable input for future numerical analysis and contribute to the development of more accurate computational models for simulating the flexural behaviour of bamboo structures.
2. MATERIALS and METHODS
The bamboo species utilized in this study was Wulung bamboo (G. atroviolacea), which was sourced from Yogyakarta, Indonesia. The selected bamboo culms, aged between 3 to 5 years, were designated as Bamboo 1, Bamboo 2, and Bamboo 3. Their geometric properties are presented in Table 4. The lengths of Bamboo 1, Bamboo 2, and Bamboo 3 are 6,245 mm, 6,240 mm, and 6,385 mm, respectively, with each culm comprising 16, 17, and 16 nodes. As shown in Table 4, the bamboo culms exhibit a non-prismatic geometry, characterized by a larger diameter at the base compared to the top.
| Speciment | Length (mm) | Diameter (mm) | Number of nodes | |||
|---|---|---|---|---|---|---|
| Bottom | Middle | Top | Average | |||
| Bamboo 1 | 624.5 | 89 | 82.5 | 79.6 | 83.7 | 16 |
| Bamboo 2 | 624 | 89.6 | 84.4 | 78.6 | 84.2 | 17 |
| Bamboo 3 | 638.5 | 89 | 80 | 70 | 79.7 | 16 |
The bamboo culms were preserved using vertical soak diffusion in a 0.2% deltamethrin solution, followed by air-drying for six months to achieve equilibrium moisture content. The relative humidity and temperature of the bamboo storage room were 85.33% and 26.05°C, respectively. After conditioning, specimens for tensile, compressive, and bending tests were prepared by cutting the culms at predetermined positions in accordance with the dimensional specifications outlined in ISO 22157: 2019. The cutting positions are illustrated in Fig. 1. The resulting tensile, compressive, and bending specimens are summarized in Table 5. Due to the limited length of the bamboo culms, the number of tensile specimens obtained from Bamboo 1, Bamboo 2, and Bamboo 3 was four, two, and two, respectively. The number of compressive specimens from Bamboo 1, 2, and 3 was two, one, and two, respectively. For the bending test, one specimen was prepared from each bamboo culm.
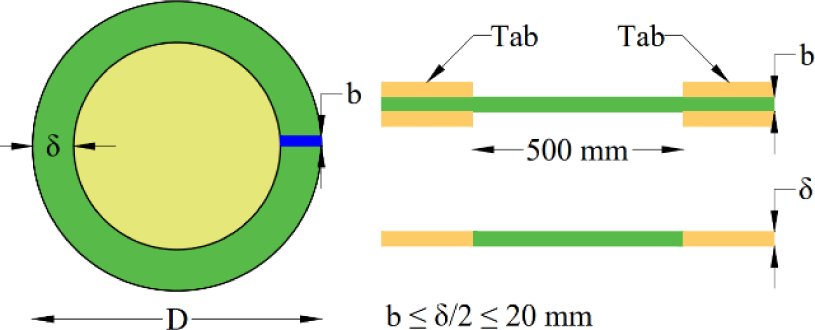
Tensile specimens were prepared in accordance with ISO 22157:2019. Their geometric configuration is illustrated in Fig. 2, and additional dimensional data are provided in Table 6. The specimen thicknesses ranged from 1.8 mm to 3.4 mm, with a gauge length of 50 mm for the tensile section. Hardwood tabs were affixed to both ends of each specimen to ensure proper gripping during testing. The tensile tests were performed using a universal testing machine, with the loading rate adjusted to produce failure within 300 ± 120 seconds.
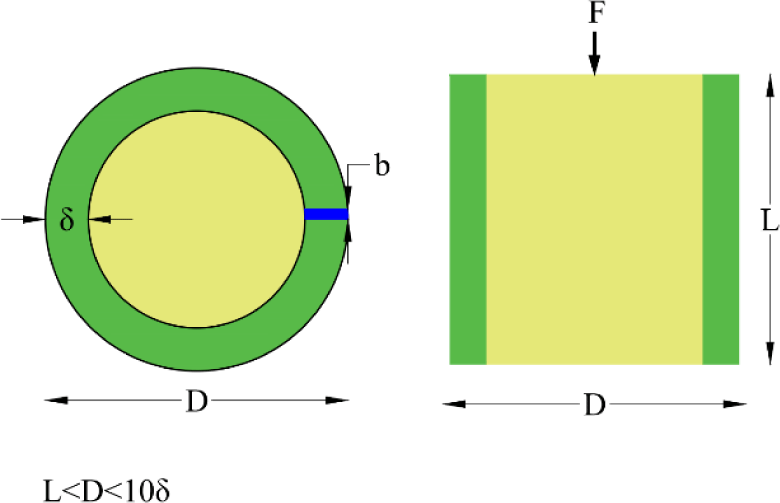
The compressive test specimens were also prepared in accordance with ISO 22157:2019. The specimen dimensions are illustrated in Fig. 3 and further detailed in Table 7. The height of each compressive specimen was approximately equal to the outer diameter of the bamboo cross-section. Compressive testing was carried out using a universal compression testing machine, with a loading rate to induce failure within 300 ± 120 seconds, similar to the tensile test procedure.
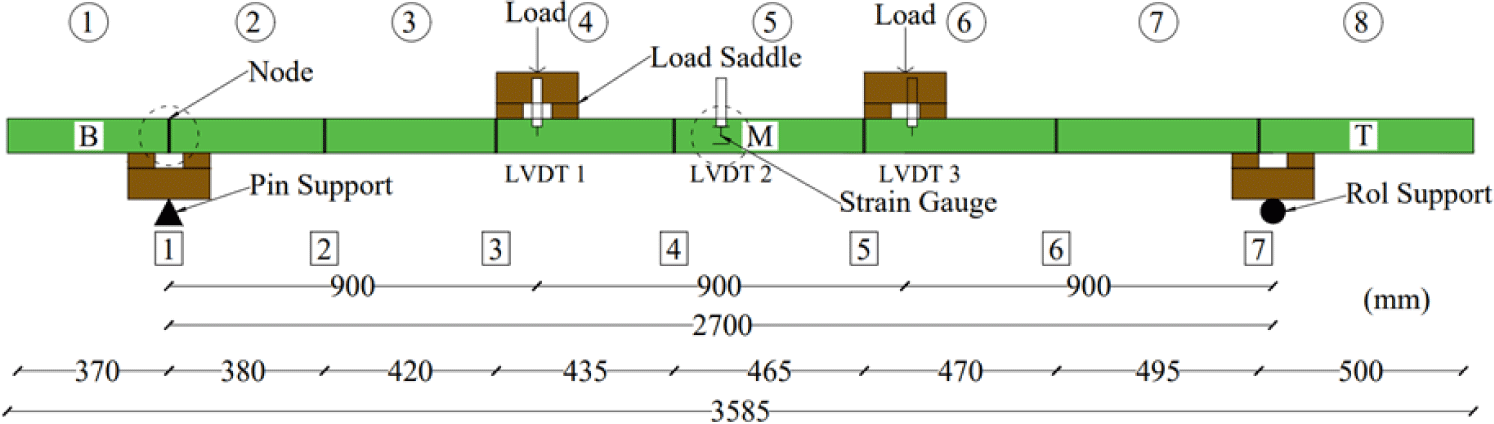
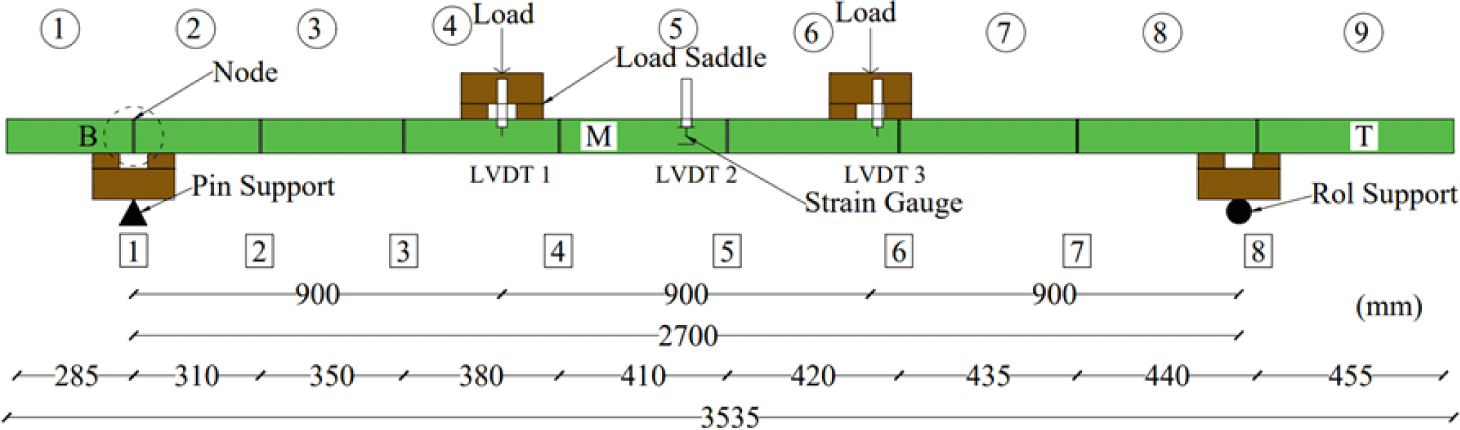
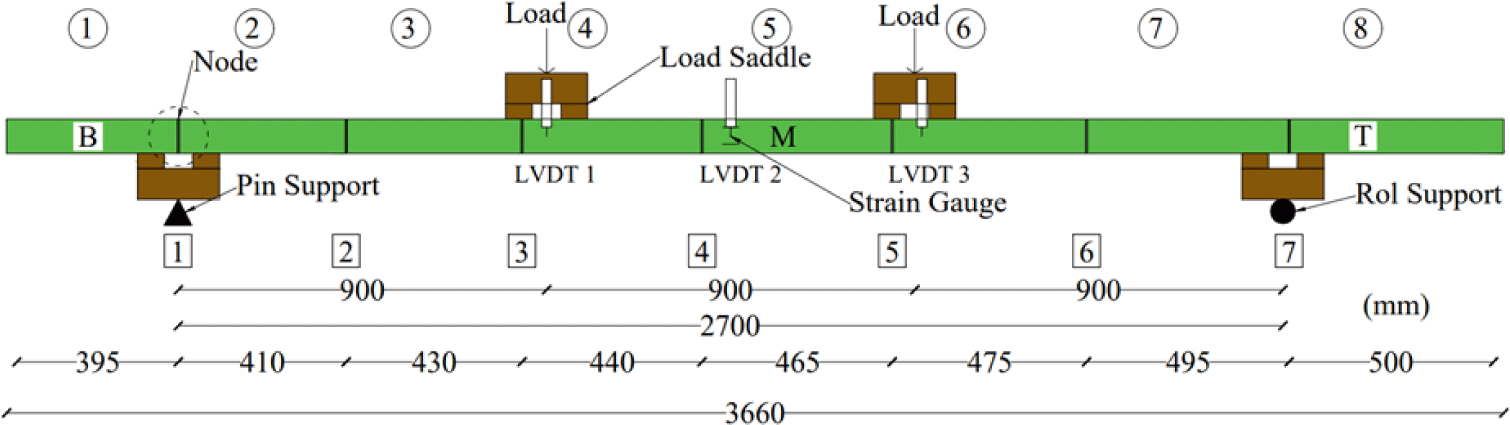
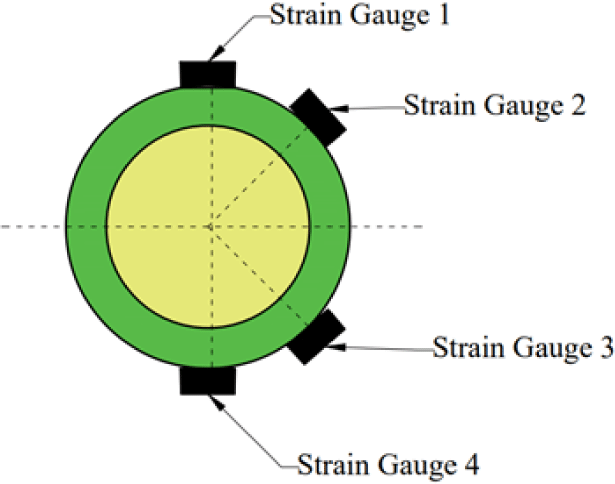
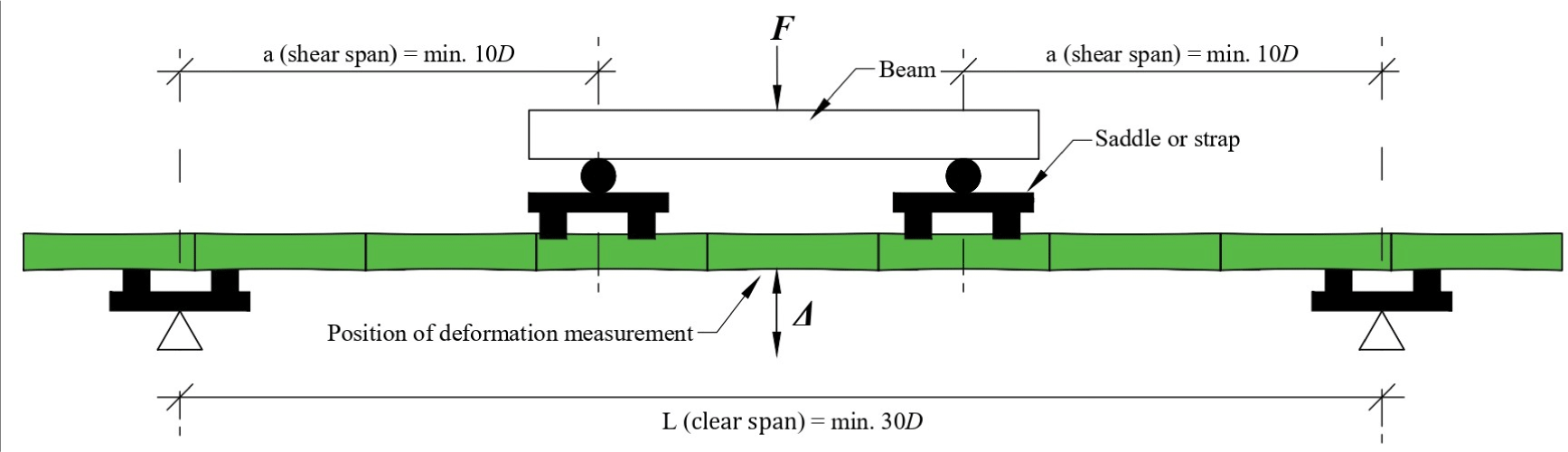
Bending test specimens were prepared from the same bamboo culms used for tensile and compressive testing. The specimen dimensions are presented in Table 8. The bending testing setups Bb1, Bb2, and Bb3 are illustrated in Figs. 4–6, respectively. These Figures show the load application points, support saddle, loading saddle, and the positions of linear variable differential transformer (LVDT). Four strain gauges were installed at the mid- span of each bamboo beam, with their positions on the cross-section detailed in Fig. 7.
3. RESULTS and DISCUSSION
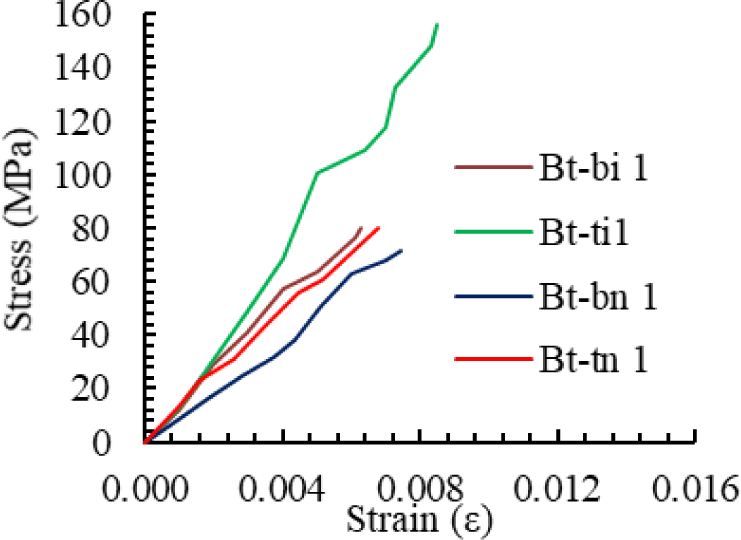
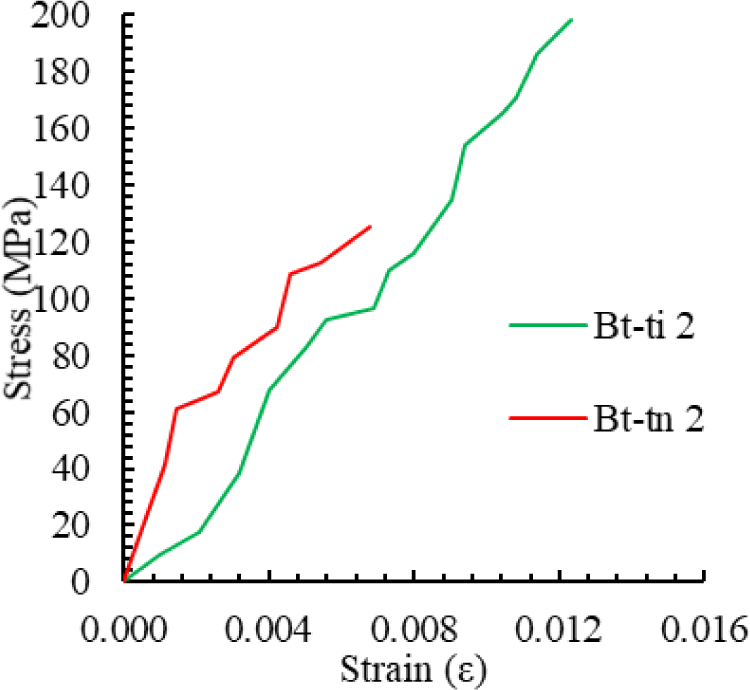
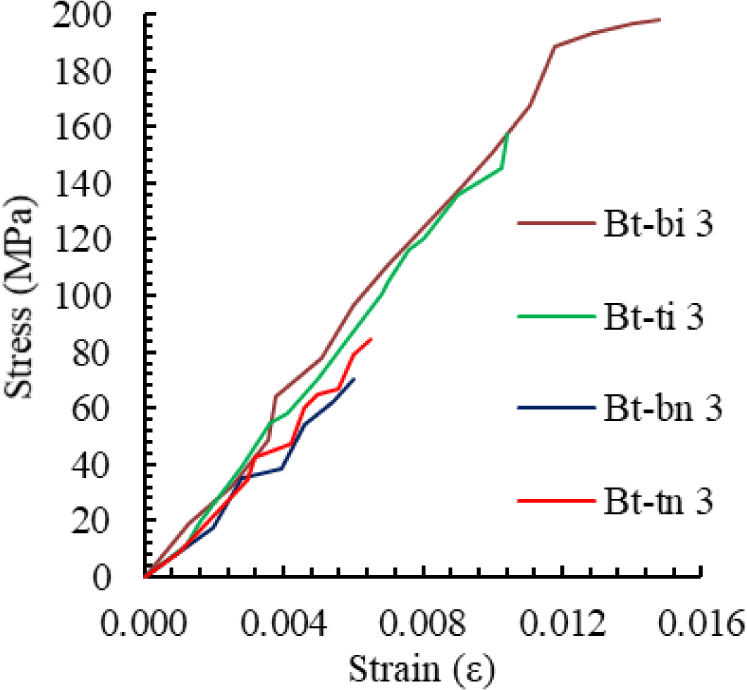
Figs. 8–10 present the tensile stress–strain curves of specimens derived from Bamboos 1, 2, and 3, respectively. The curves indicate that the tensile stress parallel to the grain of bamboo exhibits a linear behavior before failure. The ultimate tensile stress values are summarized in Table 3, ranging from 70.13 and 198.42 MPa. For Bamboo 1, the average ultimate tensile stresses of the internode and node regions were 118.08 MPa and 75.76 MPa, respectively. For Bamboo 3, the corresponding values were 177.88 MPa and 77.43 MPa. Due to specimen limitations, averaging could not be conducted for Bamboo 2; however, the ultimate tensile stresses for its internode and node parts were 198.35 MPa and 125.12 MPa, respectively. Across all specimens, the average ultimate tensile stresses of the internode and node parts were 164.77 MPa and 92.77 MPa, respectively, indicating that the internode part consistently demonstrated higher tensile strength than the node part.
The tensile elastic modulus of Wulung bamboo is presented in Table 9, awith values ranging from 9,631 to 18,400 MPa. The average modulus was determined by combining two stress–strain data pairs obtained from the bottom and part of the bamboo culm of each internode or node section of the bamboo culm. Linear regression was then applied to these combined data to calculate the average tensile elastic modulus. For Bamboo 1, the average tensile elastic modulus parallel to the grain was 16,436 MPa for the internode region and 10,607 MPa for the node region. For Bamboo 3, the corresponding values were 14,804 MPa and 12,141 MPa. Due to data limitations, averaging could not be performed for Bamboo 2; however, its tensile elastic moduli for the internode and node regions were 16,126 MPa and 18,400 MPa, respectively. Across all specimens, the average tensile elastic modulus parallel to the grain was 15,789 MPa for the internode and 13,716 MPa for the node, indicating that the internode consistently exhibited a higher modulus than the node.
The variability of the tensile test results is presented in Table 10 and was evaluated using the coefficient of variation (CoV). In contrast to the previous calculation of average tensile strength and elastic modulus, where values were determined individually for each bamboo specimen (Bamboo 1, Bamboo 2, and Bamboo 3), the variability analysis in this section was performed by grouping the data into two categories: specimens with and specimens without nodes. Consequently, each group consisted of five samples.
| Research result conducted by | This research | Hoque et al. (2019) | Cui et al. (2024) | Meng et al. (2023) | Liu et al. (2021) | |
|---|---|---|---|---|---|---|
| Tensile σ ultimate (MPa) | Number of sample without node | 5 | 3 | 320 | 6 | 147 |
| CoV internode | 30.58% | 10.38% | 24.50% | 5.42% | 6.30% | |
| Number of sample with node | 5 | 3 | - | 6 | 167 | |
| CoV node | 26.08% | 9.05% | - | 9.36% | 8.80% | |
| Tensile modulus of elasticity ET (MPa) | Number of sample without node | 5 | 3 | 320 | - | - |
| CoV internode | 13.21% | 4.12% | 15.40% | - | - | |
| Number of sample with node | 5 | 3 | - | - | - | |
| CoV node | 25.41% | 14.08% | - | - | - | |
| Compressive σ ultimate (MPa) | Number of sample without node | 3 | 4 | - | 12 | 231 |
| CoV internode | 6.76% | 9.47% | - | 7.05% | 8.20% | |
| Number of sample with node | 2 | 4 | - | 12 | 74 | |
| CoV node | 0.81% | 25.76% | - | 9.16% | 6.90% | |
| Compressive modulus of elasticity EC (MPa) | Number of sample without node | 3 | 4 | - | - | 231 |
| CoV internode | 20.25% | 40.03% | - | - | 8.70% | |
| Number of sample with node | 2 | 4 | - | - | 74 | |
| CoV node | 11.25% | 52.67% | - | - | 8.00% |
Table 10 shows that the CoV for tensile strength at the internode and node parts were 30.58% and 26.08%, respectively. The CoV for tensile modulus of elasticity at internode and node were 13.21% and 25.41%, respectively. Comparison with previous studies, also presented in Table 10, indicates that larger sample sizes do not necessarily result in lower variability in tensile properties. Two primary factors may account for this observation. First, the small cross-sectional dimensions of the tensile specimens may contribute to higher variability. Second, the irregular distribution of fibers, as noted by Al-Rukaibawi and Károlyi (2023), can also influence the results. Fiber density in bamboo varies not only along the longitudinal axis but also radially. As a result, small specimens may fail to capture representative fiber density across the bamboo cross-section, leading to greater dispersion in the measured tensile properties.
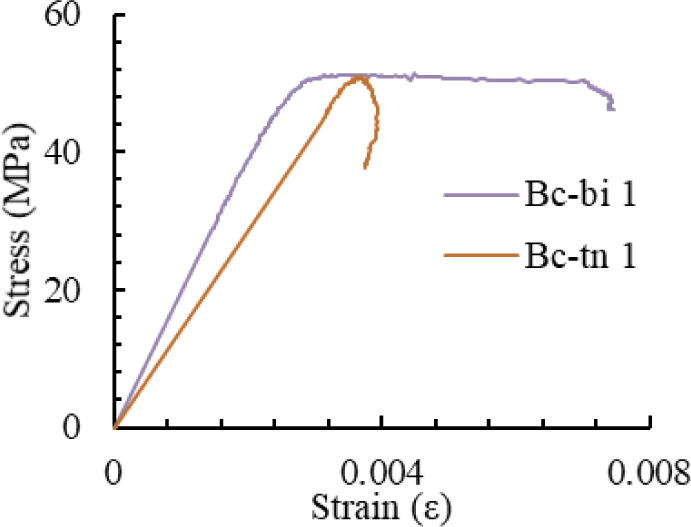
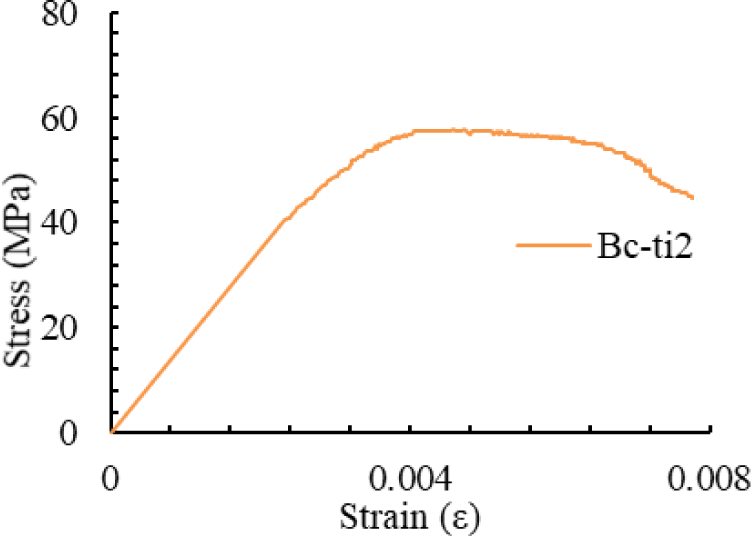
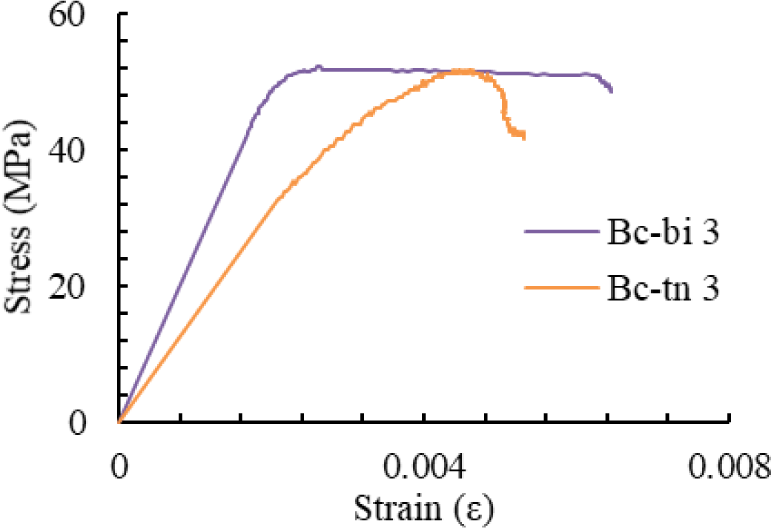
Figs. 11–13 present the compressive stress–strain curves of specimens derived from Bamboos 1, Bamboo 2, and Bamboo 3, respectively. These curves indicate that Wulung bamboo exhibits plastic behavior under compressive loading. The compressive elastic limit and ultimate stress values for each bamboo specimen are summarized summarized in Table 11.
The average compressive elastic limit stresses of the internode and node parts were 43.32 MPa and 42.90 MPa, respectively. The corresponding average ultimate compressive stresses were 53.71 MPa and 51.30 MPa. These results indicate that the internode part tends to exhibit slightly higher compressive strength than the node part.
Figs. 11–13 also illustrate that the compressive ductility of the internode part of bamboo is greater than that of the node part of bamboo. This observation is supported by the corresponding ductility index values, which are presented in Table 11. The average ductility indices of the internode and node parts were 1.894 and 1.108, respectively, confirming that the internode section of the bamboo exhibits higher compressive ductility.
The compressive elastic modulus parallel to the grain was determined from the compressive stress–strain curves, as presented in Table 11. The procedure for calculating the compressive elastic modulus differs slightly from that used for the tensile modulus. Unlike in the tensile test, the data from the top and bottom parts of each bamboo specimen were not combined due to data limitations in the compression test. For Bamboo 1, the compressive elastic moduli of the internode and node part were 19,800 MPa and 14,050 MPa, respectively. For Bamboo 2, only the internode modulus was obtained, with a value of 17,889 MPa. For Bamboo 3, the internode and node moduli were 26,120 MPa and 16,478 MPa, respectively. The average compressive elastic modulus parallel to the grain for the internode and node parts across all specimens was 21,270 MPa and 15,264 MPa, respectively. These results indicate that the internode part consistently exhibits higher compressive stiffness than the node part.
The variability of the compressive modulus and compressive strength is summarized in Table 10, where the data are categorized into two groups: internode specimens and node specimens. The compression tests were conducted on three internode samples and two node samples. The results show that the CoV for compressive strength was 6.76% for internodes and 0.81% for nodes. Meanwhile, the CoV for the compressive modulus of elasticity were 20.25% and 8.70% for internodes and nodes, respectively.
The number of compression test specimens was comparable to that of the tensile test specimens. However, the compressive mechanical properties exhibited greater homogeneity than the tensile properties. This can be attributed to the fact that compressive loading engages a larger portion of the bamboo structure, whereas tensile loading primarily acts on a limited number of fibers within the cross-section. The larger dimensions of the compression specimens allow for a more representative assessment of the material’s average compressive behavior, thereby minimizing the influence of local variations and resulting in reduced data dispersion compared to the tensile test results.
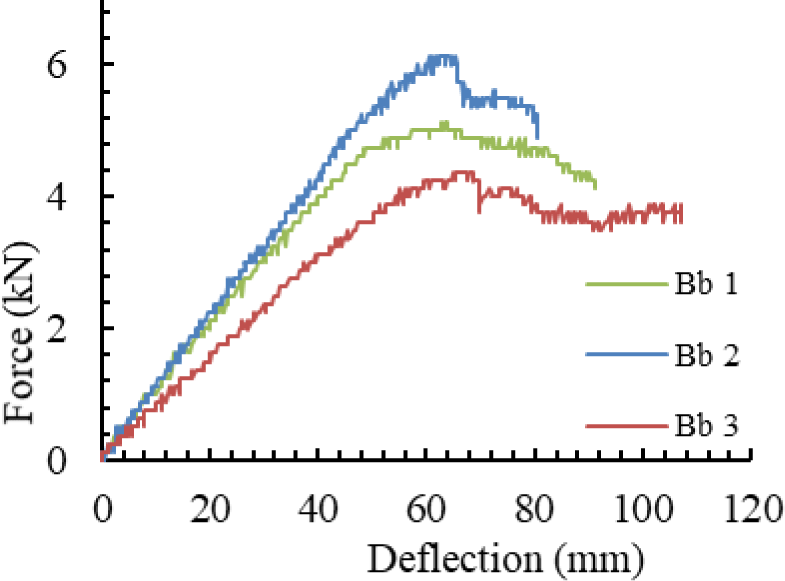
The load–deflection curves of Bb1, Bb2, and Bb3 are presented in Fig. 14. Each curve shows that the deflection of the bamboo increased linearly with load up to the elastic limit. As the load continued to increase, the deflection exhibited nonlinear growth until the ultimate load was reached. Beyond this point, the load gradually decreased.
The elastic limit load, elastic limit deflection, ultimate load, and bending elastic modulus of the three bamboo specimens are summarized in Table 12. The bending elastic modulus was determined from the slope of the load–deflection curve within the elastic range. As shown in Table 12, the average bending elastic modulus of bamboo was 18,120 MPa, with a CoV of 2.87%.
Figs. 15–17 illustrate the observed failure modes of Bamboos 1, 2, and 3, respectively. The bending failures of Bb1 (Fig. 15) and Bb3 (Fig. 17) occurred beneath the right saddle, near the top side of the specimen. In contrast, the failure of Bb2 (Fig. 16) occurred beneath the left saddle, also near the top. All specimens exhibited local buckling followed by longitudinal splitting along both edges of the bamboo culm.
Local buckling occurred because the saddle was not positioned directly over a bamboo node. Theoretically, aligning the saddle with a node can help prevent buckling. However, due to the natural variability in node spacing along the bamboo culm, consistently aligning the saddle with a node is challenging in practice. The buckling test was conducted in accordance with ISO 22157:2019, as illustrated in Fig. 18, which shows that the saddle was not precisely aligned with a node. The occurrence of local buckling influenced the bending behavior of the bamboo beam by reducing its lateral load-carrying capacity. Nonetheless, this buckling had minimal effect on the strain measurements in this study, as it occurred near the saddle—approximately one-third of the span—whereas the strain gauges were installed at mid-span, away from the buckling zone.
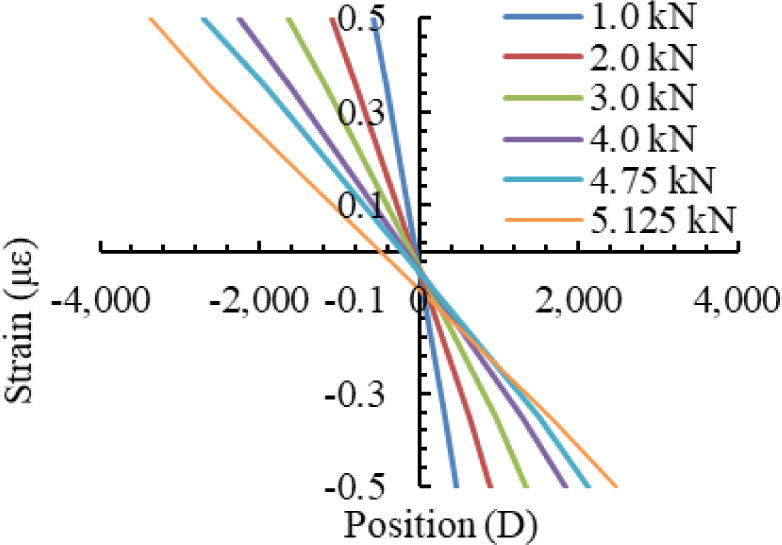
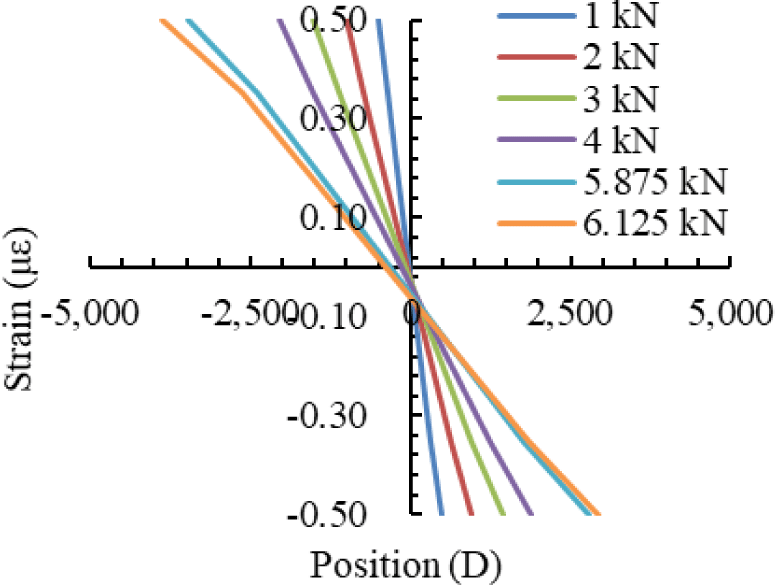
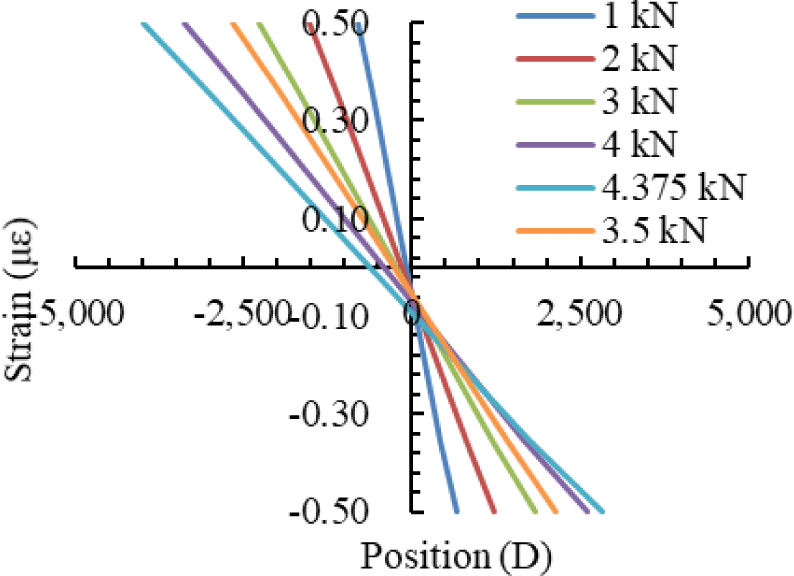
The strain distribution curves of specimens Bb1, Bb2, and Bb3 under lateral loading from 1 kN to the ultimate load are presented in Figs. 19–21, respectively. In all cases, the strain distribution remained approximately linear, even beyond the elastic limit. These curves were used to determine the position of the neutral axis at various load levels. The neutral axis was identified as the location along the cross-section where the longitudinal strain equaled zero, and its position was measured relative to the mid-diameter of the bamboo culm. As shown in Figs. 19–21, the neutral axis positions of Bamboos 1, 2, and 3 at different loading stages are summarized in Table 13. Notably, the neutral axis position varied with increasing load and tended to shift away from the centroid of the cross-section. Overall, the compressive strain zone was consistently larger than the tensile strain zone, indicating an asymmetric flexural response of the bamboo culm.
The neutral axis does not lie at the mid-diameter of the bamboo cross-section due to the difference between the tensile and compressive moduli of elasticity parallel to the grain. For the internode region, the average tensile and compressive moduli are 15,789 MPa and 21,270 MPa, respectively. In the node region, the corresponding values are 13,716 MPa and 15,264 MPa.
The reduced stiffness in the node area is attributed to both microstructural and morphological factors. The discontinuity and interruption of longitudinal fibers within the node restrict the efficiency of stress transfer, particularly under tensile loading (Chen and Luo, 2020). Moreover, the irregular and multidirectional fiber orientations in the node region leads to localized stress concentrations and deformation, thereby diminishing its structural integrity (Meng et al., 2023).
Further analysis of the neutral axis position focused on the tensile and compressive properties parallel to the grain in the internode part, as the strain gauges were installed in this section of the bamboo culm. The results indicate that the tensile elastic modulus in the internode is lower than its compressive counterpart, consistent with findings reported by Gauss et al. (2019). However, the observed position of the neutral axis—located below the mid-height of the cross-section—would theoretically suggest that the tensile modulus should exceed the compressive modulus.
The discrepancy between the tensile-to-compressive modulus ratio and the observed neutral axis position can be attributed to two primary factors. First, bamboo is an inherently non-homogeneous material, with mechanical properties that vary along its length due to differences in fiber distribution, density, and anatomical structure between nodes and internodes. Second, tensile, compressive, and bending specimens could not be extracted from the same longitudinal location along the culm due to dimensional constraints. This limitation poses a significant challenge in structural bamboo research, particularly when attempting to establish a direct correlation between the neutral axis position and the tensile and compressive moduli of elasticity parallel to the grain.
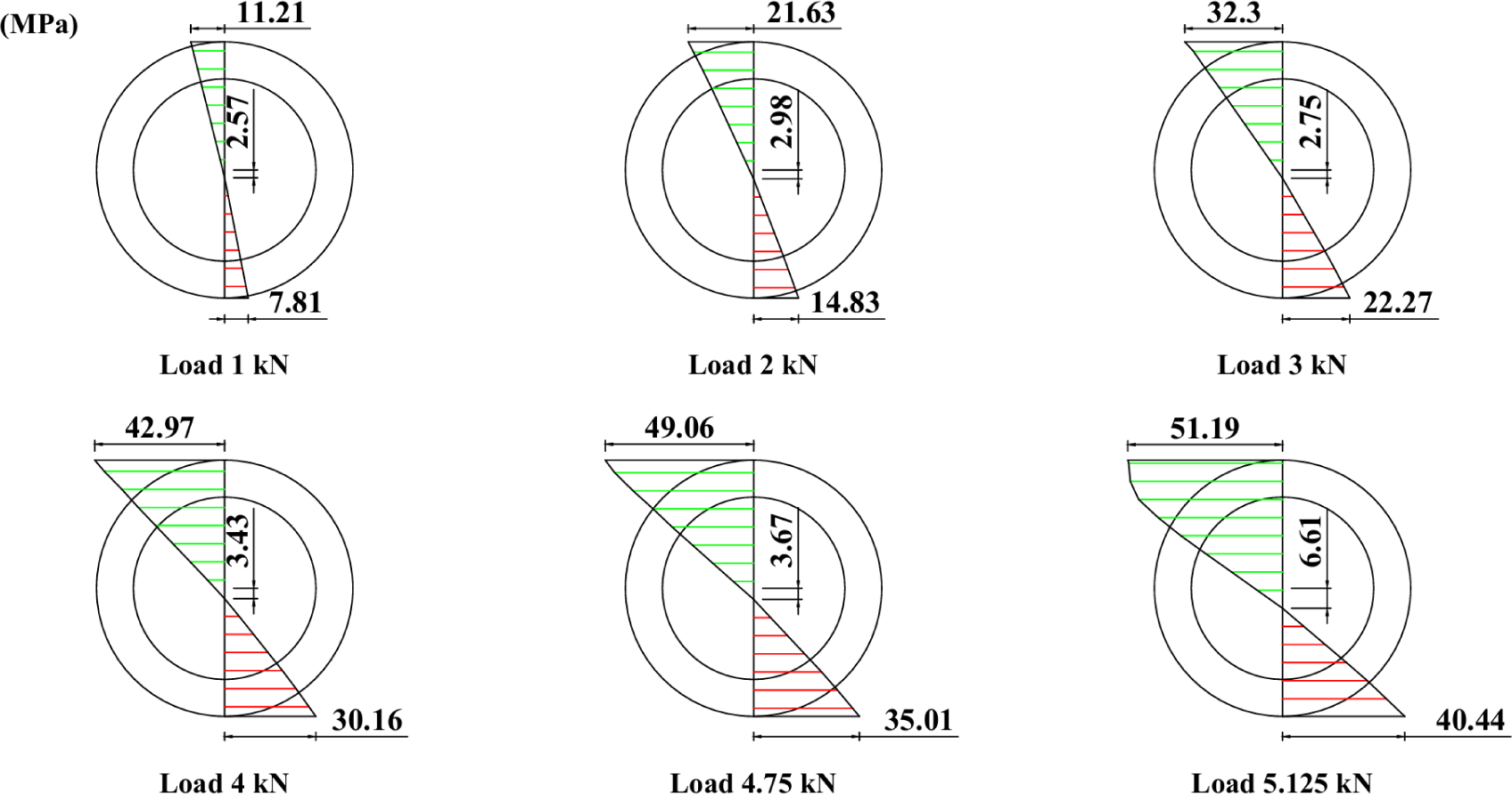
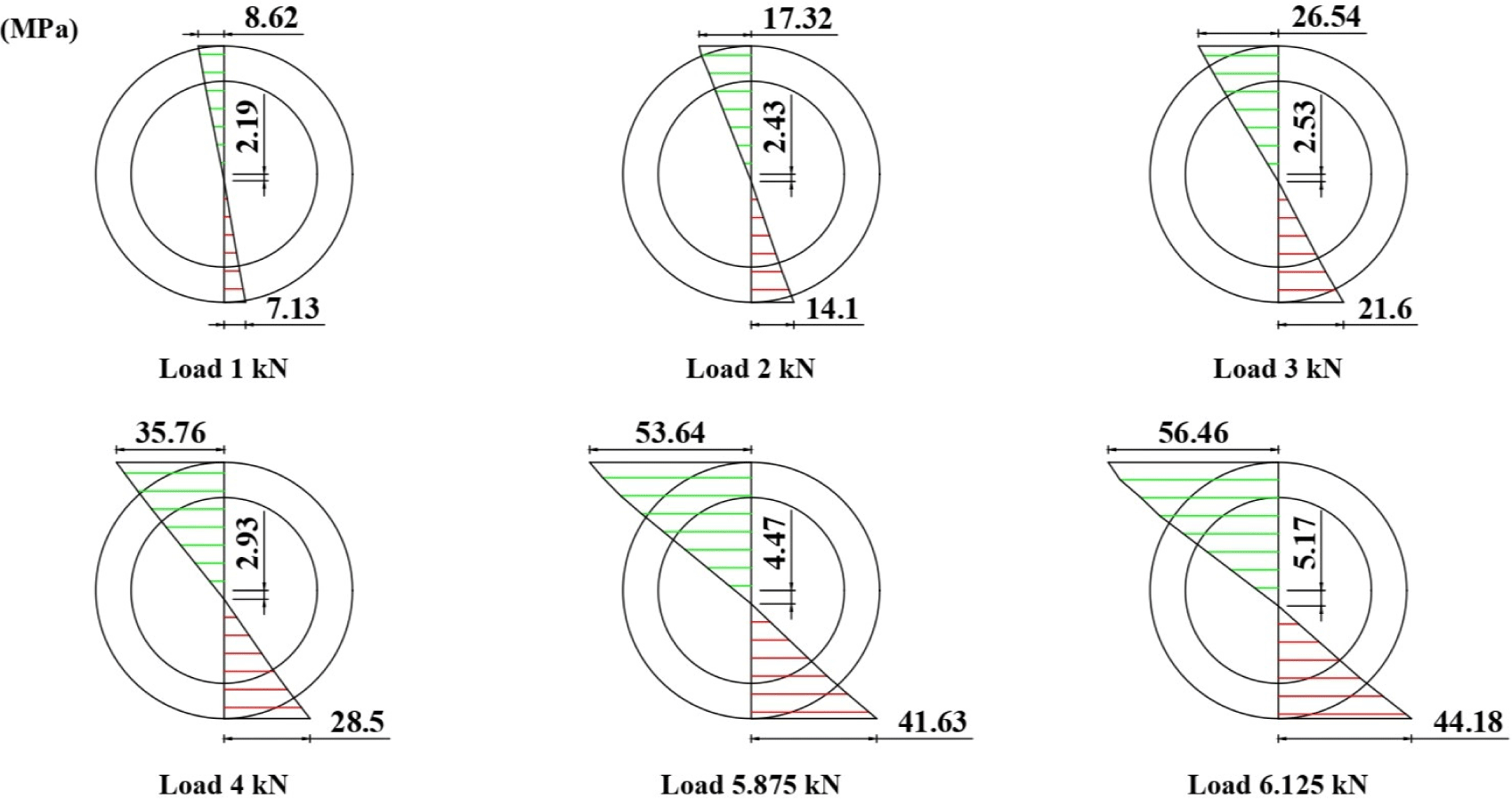
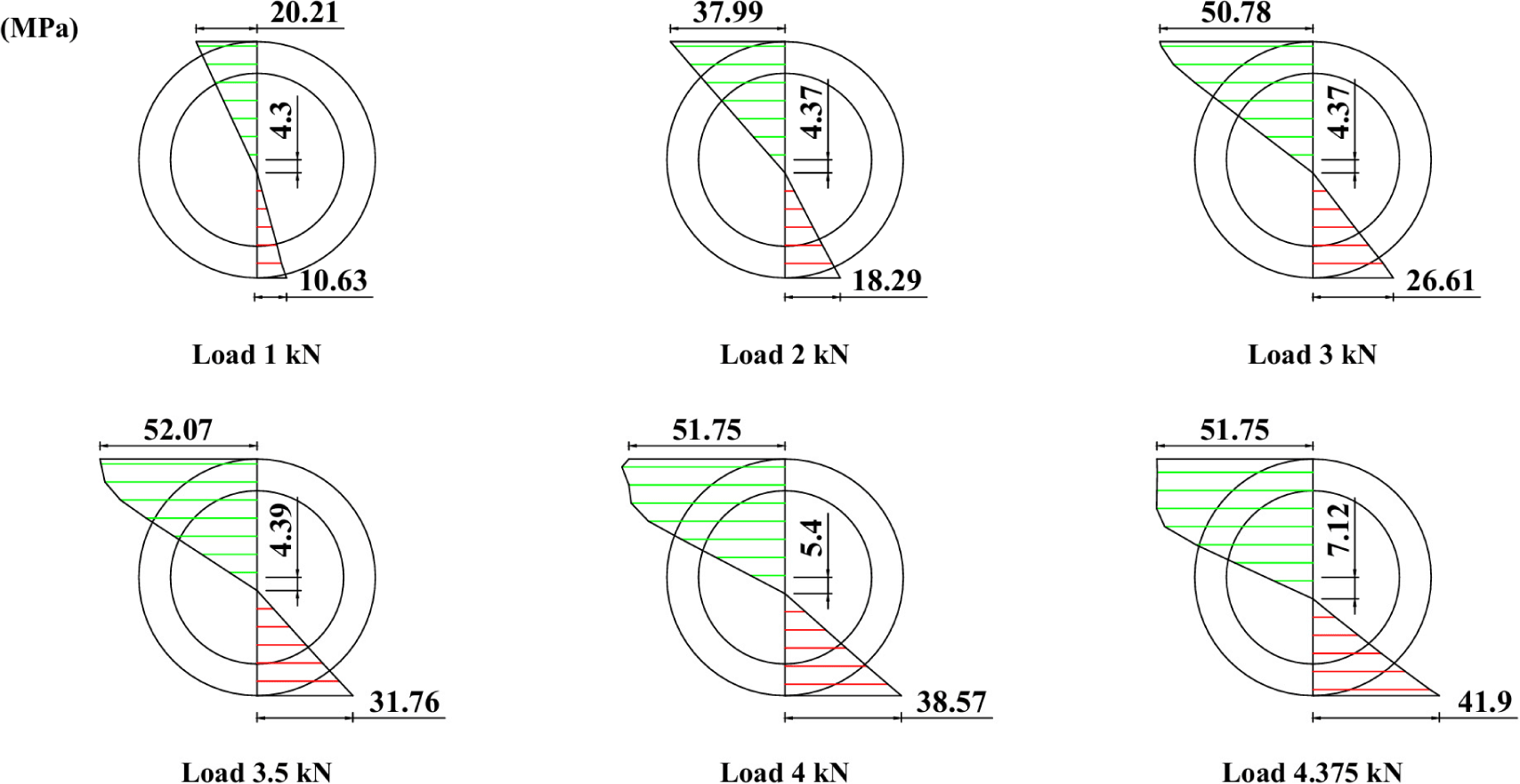
In addition, this study conducted an analysis of strain distribution, stress distribution, and the equilibrium of normal forces at the cross-section where the strain gauges were installed. The stress distributions for specimens Bb1, Bb2, and Bb3 under various loading conditions are presented in Figs. 22–24. These distributions were derived from the average stress–strain relationships obtained from the tensile and compressive tests parallel to the grain in the internode region of each bamboo culm and correlated with the strain distributions across the respective cross-sections (Figs. 19–21). Within the linear range, the stress–strain relationship was defined by the average modulus of elasticity, as shown in Table 14. Based on these stress distributions, the axial tensile force the axial tensile FT and compressive forces FC were calculated. The results are presented in Tables 15–17 for Bamboos 1, 2, and 3, respectively.
| Bamboo | ET internode (MPa) | Average ET internode (MPa) | EC internode (MPa) |
|---|---|---|---|
| Bb1 | 12,937 | 15,368 | 19,800 |
| 17,799 | |||
| Bb2 | 16,126 | 16,126 | 17,889 |
| Bb3 | 13,407 | 14,268 | 26,120 |
| 15,129 |
The results indicate that the resultant axial force (ΣF) does not equal zero when the axial tensile FT and compressive FC forces are calculated using the original tensile and compressive moduli of elasticity obtained from the tests. Theoretically, the resultant axial force must be zero. As previously discussed, when the neutral axis shifts downward, the tensile modulus should exceed the compressive modulus to achieve axial force equilibrium. To address this discrepancy, a modification factor was introduced in this study. The applied modification factors and the corresponding adjusted axial force results are presented in Tables 15–17. By applying this factor, the tensile modulus becomes greater than the compressive modulus, thereby bringing the resultant axial force closer to zero. Further detailed analysis using finite element modeling is recommended to simulate the interaction between neutral axis position, the modified tensile and compressive moduli of elasticity parallel to the grain, and the overall bending behavior of bamboo.
In the structural design of bamboo beams based on ISO 22156:2021, the allowable lateral load is primarily determined by the flexural strength, while axial tensile and compressive strengths are generally not considered. However, ISO 22156:2021 does not yet specify the correction factors, as specified in the timber structural standard code. Thus, a review of bamboo beam design in this study was conducted by calculating the allowable lateral load for each specimen using the Load and Resistance Factor Design (LRFD) method. The flexural strength values of Bamboos 1, 2, and 3 were used as their respective reference strengths. A flexural resistance factor (ϕ) of 0.85 was applied, in accordance with SNI 7973:2013, which is adapted from NDS 2012. All modification factors—including wet service, temperature, beam stability, size, flat use, incising, repetitive member, format conversion, and time effect factor—were assumed to be equal to 1.0. The allowable lateral loads were then calculated following ISO 22156:2021 and are summarized in Table 18. As shown, the calculated values remain below the corresponding experimental elastic limit loads. This indicates that the normal stress distribution parallel to the fibers remains linear and that the structural response of the bamboo beams remains within the elastic range. Considering these calculation results, ISO 22156:2021 can be appropriately applied at the design stage, provided that the material behavior remains within the linear elastic domain. Nevertheless, incorporating a more detailed analysis of the actual stress-strain distribution along the fiber direction would help support and refine the structural design process.
| Specimen | Experiment result | Allowable lateral load (kN) | ||
|---|---|---|---|---|
| Pelastic-limit (kN) | Δelastic-limit (mm) | Pultimate (kN) | ||
| Bb1 | 4.75 | 8.475 | 5.125 | 4.356 |
| Bb2 | 6.00 | 6.250 | 6.125 | 5.206 |
| Bb3 | 3.50 | 5.450 | 4.375 | 3.719 |
4. CONCLUSIONS
The average tensile modulus of elasticity parallel to the fibers of Wulung bamboo was 15,789 MPa for internodes and 13,716 MPa for nodes, whereas the average compressive modulus of elasticity in the same direction was 21,270 MPa and 15,264 MPa, respectively. This disparity between tensile and compressive stiffness leads to a shift in the neutral axis position when the bamboo is subjected to lateral loading, causing it to deviate from the centroid of the cross-section.
The results of the bending tests indicate that the strain distribution across the bamboo cross-section remains linear, even beyond the elastic limit. The neutral axis was consistently observed below the geometric center of the cross-section. Moreover, the position of the neutral axis shifted downward as the magnitude of lateral loading increased. When the applied load remained within the elastic range, the stress distribution was also linear throughout the cross-section. However, once the load exceeded the elastic limit, the stress distribution became nonlinear, particularly in the compressive region above the neutral axis.
The experimental results revealed that the average tensile modulus of elasticity is lower than the average compressive modulus of elasticity. Nevertheless, the neutral axis was found to lie below the centroid of the bamboo cross-section. Theoretically, such a position implies that the tensile modulus should exceed the compressive modulus in order to achieve equilibrium of internal normal forces within the beam. To address this inconsistency, a modification factor for the elastic moduli was introduced in this study to ensure a balanced stress distribution and satisfy equilibrium conditions in flexural analysis.
The observation of bending behavior, particularly in establishing a direct correlation between the neutral axis position and the tensile and compressive moduli of elasticity parallel to the grain, presents significant challenges. One of the main obstacles is the limitation of specimen dimensions, which makes it difficult to obtain tensile and compressive specimens parallel to the grain from the exact location where strain gauges are installed. Furthermore, bamboo is inherently non-homogeneous in both the radial and longitudinal directions, further complicating accurate characterization of its mechanical behavior.
Further finite element analysis is recommended to simulate the interaction between the neutral axis position, the modified tensile and compressive moduli of elasticity parallel to the grain, and the overall bending behavior of bamboo. This simulation should incorporate the proposed modification factors introduced in this study. These modification factors can be applied to the constitutive equation of bamboo as input material properties to more accurately represent its mechanical response under flexural loading.
Based on the design review conducted in accordance with ISO 22156:2021, the calculated allowable loads remain within the linear range, and the structural response of the bamboo beams remains in the elastic domain. These results suggest that ISO 22156:2021 can be reliably applied during the design phase, provided that the material behavior does not exceed the linear elastic range. However, incorporating a more detailed analysis of the actual stress–strain distribution along the fiber direction would further enhance the accuracy and reliability of the structural design process.