Journal of the Korean Wood Science and Technology

The Korean Society of Wood Science & Technology

J. Korean Wood Sci. Technol. 2025; 53(3):207-224

pISSN: 1017-0715, eISSN: 2233-7180

DOI: https://doi.org/10.5658/WOOD.2025.53.3.207

Original Article

Effect of Thickness and Lamina Species Combination on Bending and Shear Properties of Cross Laminated Timber (CLT) Panel

Kundari RAHMAWATI¹^,^†

, Achmad BASUKI¹, Halwan Alfisa SAIFULLAH¹, Buan ANSHARI², Tafidah Khairiyyah SAHARSO¹

¹Department of Civil Engineering, Faculty of Engineering, Sebelas Maret University, Surakarta 57126, Indonesia

²Department of Civil Engineering, Faculty of Engineering, Mataram University, Mataram 83115, Indonesia

^†Corresponding author: Kundari RAHMAWATI (e-mail: kundari.rahmawati@staff.uns.ac.id)

Copyright 2025 The Korean Society of Wood Science & Technology. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Nov 21, 2024; Revised: Dec 26, 2024; Accepted: Feb 27, 2025

Published Online: May 25, 2025

ABSTRACT

Cross-laminated timber (CLT) is an innovative engineered timber material used in the research and development phase in Indonesia. Therefore, the characteristics of CLT based on local timber species must be investigated in depth. The purpose of this study was to investigate the effects of the thickness and lamina species combination of local timber on the bending stiffness and shear stress of CLT. CLT with two different thicknesses of 51 mm (17/17/17 mm) and 67 mm (25/17/25 mm) and two different lamina configurations of acacia CLT and a combination of two species Acacia mangium (acacia) and Melia azedarach (mindi) became a hybrid CLT. An increase in the acacia CLT thickness had a positive effect on the bending stiffness. The bending stiffness of acacia CLT with a thickness of 67 mm was 3.77 times higher than that of acacia CLT with a thickness of 51 mm, whereas in hybrid CLT, it increased by 3.38 times. In terms of shear stress, the effect of thickness was not significant on Acacia CLT, as it showed a decrease of 0.01 MPa, whereas hybrid CLT experienced a reduction of 0.29 MPa, which is approximately 19.71%. The bending stiffness test results on CLT with uniform lamina thickness can be predicted using popular theoretical approaches, such as Shear analogy, Gamma theory, and Timoshenko theory. Meanwhile, the prediction of the shear stress using the Shear analogy was the closest to the test results for the entire CLT configuration.

Keywords: cross-laminated timber (CLT); effect thickness; lamina species; bending stiffness; shear strength

1. INTRODUCTION

The development of structurally engineered timber technology in Indonesia is relatively limited, although Indonesia has many wood species that can be utilized as raw materials in the engineered timber industry. Structurally engineered timber was engineered wood that functions as the main element in building construction, such as columns, beams, floor plates, shear walls, and roofs. Cross-laminated timber (CLT) is an engineered timber that offers the strength and stability required for its main structural elements. Globally, various timber species have been studied for their role in CLT production. Radiata pine timber produced CLT panels with bending and shear strengths exceeding the characteristic strength of the raw material (Li et al., 2020; Navaratnam et al., 2020). Southern pine, which is used as a raw material for CLT panels, produces bending and shear strengths that exceed V3 standards (Hindman and Bouldin, 2015). Hematabadi et al. (2020) observed bending and shear using poplar wood, and the results showed that the span-to-depth ratios were directly proportional to the moduli of rupture and elasticity in the major and minor strength directions. Crovella et al. (2019) conducted experiments using three types of wood: Eastern White Pine, Red Maple, and White Ash. The results showed that the bending stiffness, bending strength, and shear strength of hardwood were higher than those of softwood with the same lamina composition.

A hybrid CLT with outer layer hinoki (spruce, Chamaecyparis obtusa) and middle layer and sugi (Japanese cedar, Cryptomeria japonica) middle layer was conducted by Ukyo et al. (2021); the amount of rolling shear stress in the cross layer was 0.9–1.1 times the average shear stress, which was negatively correlated with the nominal shear strength. The use of hardwood improved the softwood characteristics of the hybrid CLT system in terms of both the bending stiffness and shear strength (Ma et al., 2021; Yang et al., 2021). Trisatya et al. (2023) recommended positioning high-density wood as the outer layer of hybrid CLT.

The tropical timber species investigated by Hariz et al. (2023) resulted in flexural mechanical properties of the puspa-acacia-puspa hybrid CLT equivalent to acacia CLT and had a shear strength that met the JAS 3079 standards. Galih et al. (2020) composited acacia with bamboo into a CLT material, and the results showed that the elastic modulus was 2.73 times higher than that of CLT using spruce pine fir (SPF) and the shear modulus was 0.8 lower than that of SPF CLT.

When using new wood species for the mass production of CLT, it is necessary to investigate the consistency of the theoretical models used to predict strength and stiffness (Crovella et al., 2019). Brandner et al. (2016) also emphasized that the consistency between the design and experimental methods used to predict the strength and stiffness must be proven accurately. However, the technical information on CLT based on tropical wood species from Indonesia is limited. Consistent theoretical models for predicting the strength and stiffness of CLT panels have not yet been developed; therefore, investigations on this matter are urgently needed.

Previous research on CLT has focused on the bending stiffness, bending strength, and shear strength of CLT with uniform lamina thickness. The diversity of lamina thicknesses in the CLT resulted in different stress distributions and affected the bending stiffness and shear resistance. This study aims to analyze the effects of different combinations of thickness and wood species on the mechanical performance of CLT to find more efficient and sustainable design solutions for modern construction applications. This study also provides an overview of the theoretical approaches that can be used to predict the stiffness and strength of CLT panels with different thickness configurations and lamina species.

2. MATERIALS and METHODS

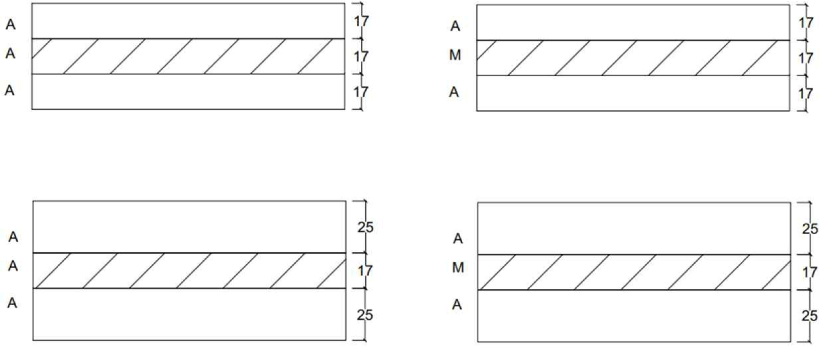
The materials used in this study were acacia and mindi species obtained from commercial wood suppliers in Indonesia. The specimens were categorized into two groups: one based on layer thickness and the other based on material composition, for example, acacia CLT and hybrid CLT. In the acacia CLT 3 (A-CLT/3) specimens, all layers used acacia timber with an average density of 0.622 g/cm³ (COV 0.07), whereas the hybrid CLT specimens (H-CLT/3) had longitudinal layers made of acacia and transverse layers made of mindi with an average density of 0.420 g/cm³ (COV 0.12). Based on the thickness of the layers, there were 3-layer CLT with a thickness of 17 mm for each layer and 3-layer CLT with a thickness of 25 mm for the longitudinal layer and 17 mm for the transverse layer (Fig. 1). The laminae used had a width of 100 mm and an average moisture content of 12%. Then the panels were conditioned for four weeks at 65 ± 5% RH. Polyurethane was used as the adhesive with a gluing spread of 160 g/m². Pressing was performed using a hydraulic cold press for 1 h at a pressure of 1.20 N/mm². From the preliminary tests referring to ASTM (2014), the modulus of elasticity (MOE) of acacia was obtained, with the tensile test yielding E₀ = 14,832.16 MPa (COV = 0.14, n = 15) and the bending test providing E₉₀ = 7,622.23 MPa (COV = 0.13, n = 15) and for mindi E₀= 10,380.36 MPa (COV 0.13, n=10); E₉₀= 3,461.08 MPa (COV 0.14, n = 10). The CLT were produced with dimensions of 1,200 × 2,400 mm and then cut according to the dimensions required of the type of testing performed.

Fig. 1. Layer configuration of the tested CLT. A: acacia, M: mindi, CLT: cross-laminated timber.

Download Original Figure

2.1. Bending test of cross-laminated timber

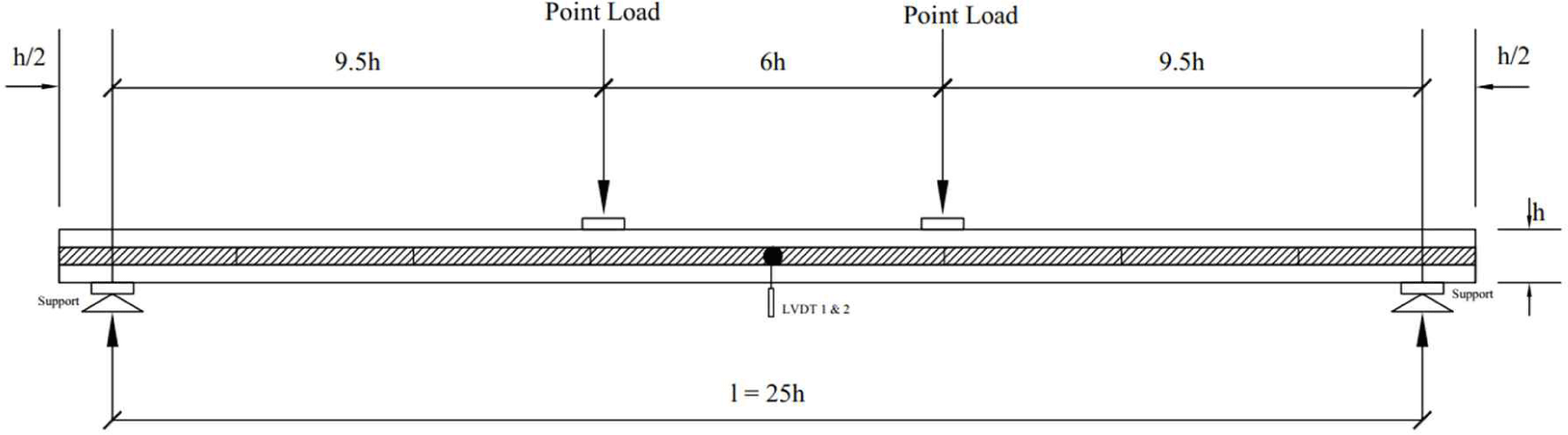
The acacia CLT was subjected to a four-point bending test with a ASTM (2015) span-to-depth ratio (R_sd) of 1:25, and the loading configuration is illustrated in Fig. 2 and Table 1. The loads and deflections were recorded using a data logger. The global deflection (w_global) was measured using longitudinal linear variable differential transformers (LVDTs) mounted at the midspan on both sides of the CLT panel. The panel was loaded constantly on the major axis at a displacement speed of 5 mm/min using an actuator equipped with a 100 kN load cell. The details of the CLT bending specimens are presented in Table 1.

Fig. 2. Configurations of the bending test of CLT. CLT: cross-laminated timber.

Download Original Figure

Table 1. Details of CLT bending specimens

Sample ID	Lamina layups (mm)	Thickness (h, mm)	Span (l, mm)	Width (b, mm)	R_sd	NoS
A-CLT3/51	17/17/17	51	1,275	300	1:25	3
A-CLT3/67	25/17/25	67	1,675	300	1:25	3
H-CLT3/51	17/17/17	51	1,275	120	1:25	5
H-CLT3/67	25/17/25	67	1,675	120	1:25	5

CLT: cross-laminated timber.

Download Excel Table

The bending strength or modulus of rupture (MOR) of each specimen was calculated using the force equilibrium theory presented in Equation (1) and MOE in Equation (2).

M O R = 3 F max (l − l ′) 2 b h 2

(1)

M O E = (F 1 − F 2) a (w 2 − w 1) 4 b h 3 (3 l 2 − 4 l ′ 2)

(2)

Where F_max is the ultimate load capacity, l is the span between the supports, l′ is the distance between the loading points, a is the distance between the support and loading point, F₁ and F₂ are 10% and 40% of F_max, respectively, and w₁ dan w₂ the global displacements under the F1 and F2 conditions, respectively. G is the shear modulus, b is the width of the specimen, and h is the thickness. The global stiffness (EI_G) of each specimen was calculated using Equation (3),

E I G = 3 a l 2 − 4 a 2 48 (w 2 − w 1 F 2 − F 1 − 3 a 5 G b h)

(3)

2.2. Shear test of cross-laminated timber

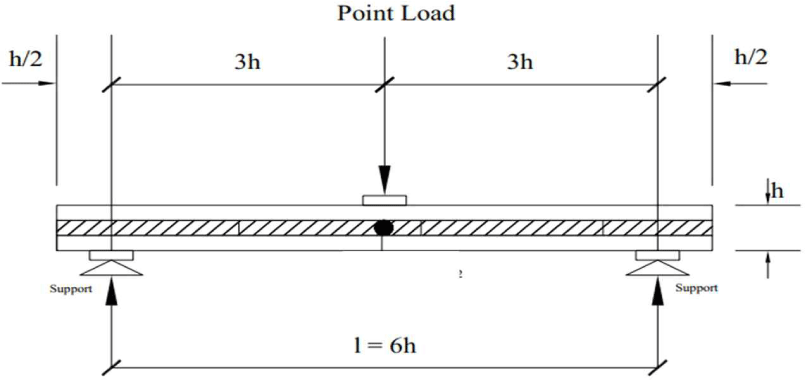
The determination of the shear properties of CLT 3 in this study was based on a ASTM (2015) short-span bending test with a span-to-depth ratio (R_sd) of 1:9, as shown in Fig. 3. The details of the specimen dimensions used in the shear tests are summarized in Table 2.

Fig. 3. Configurations of the shear test of CLT. CLT: cross-laminated timber.

Download Original Figure

Table 2. Details of CLT bending specimens

Sample ID	Lamina layups (mm)	Thickness (h, mm)	Span (l, mm)	Width (b, mm)	R_sd	NoS
A-CLT3/51	17/17/17	51	306	140	1:6	3
A-CLT3/67	25/17/25	67	402	140	1:6	3
H-CLT3/51	17/17/17	51	306	120	1:6	3
H-CLT3/67	25/17/25	67	402	120	1:6	3

CLT: cross-laminated timber.

Download Excel Table

The shear stress of the CLT obtained from the bending test was calculated using Equation (4), where τ_r is the maximum shear stress (MPa), F_max is the maximum load from the test, b is the panel width, and h is the thickness of the CLT panel.

τ r = 3 F max 4 b h

(4)

2.3. Analytical approach

The stiffness calculation approach (EI) for the CLT, which was assumed to be an isotropic material, was calculated using Equation (5) (Karacabeyli and Gagnon, 2019).

E I g r o s s = E 1 b h 3 12

(5)

Where EI_gross is the bending stiffness by gross cross section, E₁ is the MOE of the outer layer, b and h are the width and thickness of the CLT specimen, respectively.

Unlike the isotropic approach, the Timoshenko beam theory is an extension of the Bernoulli–Euler beam theory used to calculate shear deformations in composite beams. It utilizes a shear form factor k to correct the cross-sectional shear stiffness and does not assume that the cross-section remains straight and perpendicular to the neutral axis (Ehrhart and Brandner, 2018; Rahman et al., 2020). The effective bending stiffness and shear stress of the laminated beams were calculated using Equations (6) and (7), respectively (Brandner et al., 2016; Wallner-Novak, 2014).

E I e f f = ∑ i n (E i . I i + E i . A i . z i 2)

(6)

τ r = V . ∑ i n (E i . A i . z i) E I e f f . b

(7)

Another popular analytical approach is the Gamma method. The Gamma method describes the longitudinal layer as a beam and the transverse layer as a constantly distributed connection. It was assumed that the stiffness was loaded only on the transverse layer, which was identical to the rolling shear modulus (Huang et al., 2023b). In determining the contribution of shear deformation to deflection due to buckling, factor γ_i used to measure the efficiency of layer-to-layer interactions (Huang et al., 2023a). Subsequently, the effective bending stiffness and shear stress of the laminated beam were calculated using Equations (8) and (9), respectively (Ehrhart and Brandner, 2018):

E I e f f = ∑ i n (E i . I i + γ i . E i . A i . z i 2)

(8)

Where

γ i = (1 + π 2 . E i . A i ι r e f 2 . h i G r . b) τ r = V . ∑ i n (γ i E i . A i . a i) E I e f f . b

(9)

Other methods, such as shear analogy (SA), describe the layer panel as two systems composed of beam imaginers A and B (Christovasilis et al., 2016). The total inherent bending stiffness of the different layers was applied to Beam A along its neutral axis, whereas Beam B received the total shear stiffness of all layers, the neutral axis of the overall bending, and the combined bending stiffness of all layers and connections alone. Because the two beams were connected by a virtual beam composed of continuously dispersed link elements with unlimited axial rigidity, equal deformation at each point along the beam when carrying the transverse load had to be verified (Huang et al., 2023b). Subsequently, the effective bending stiffness and shear stress of the laminated beam were calculated using Equations (10) and (11) (Ehrhart and Brandner, 2018):

E I e f f = B A + B B

(10)

where

B A = ∑ i n E i . I i B B = ∑ i n E i . A i . I i . z i 2 τ r = V . ∑ i n (E i . A i . z i) B B . b

(11)

Where A_i is the cross-sectional area of each layer A_i = h_i.b and Ei are the elastic moduli of each layer: E_i = E₀ for the longitudinal layer and E_i = E₉₀ = 0 for the transverse layers. I is the moment of inertia z_i is the distance between the center of each layer and the center of the entire cross-section; V is the shear capacity obtained from short-span bending test; b is the width of the CLT panel; and a_i distance between the center of each layer and the gravity center of the total cross-section; l_reff is the reference span of the beam (Wallner-Novak, 2014). h_i is the thickness of the layer in the direction transverse to the load (Karacabeyli and Gagnon, 2019). B_A and B_B denote the bending stiffness values.

3. RESULTS and DISCUSSION

3.1. Bending test

The bending test results are listed in Table 3. Maximum load (F_max); mid-span ultimate moment (M_max); Δ_max is the deflection at ultimate load taken from global measurements; and global MOE (E_g).

Table 3. Results of the bending test of acacia CLT

Test no	F_max (kN)	V_max (kN)	M_max (kN.m)	Width (mm)	Δ_max (mm)	MOR (MPa)	E_g (MPa)
A-CLT3/511	48.99	24.49	11.24	300	31.73	62.44	13,532.79
A-CLT3/511	49.70	24.85	11.41	300	32.73	63.35	13,391.13
A-CLT3/511	38.09	19.04	8.74	300	24.03	48.55	14,392.91
Mean			10.46			58.11	13,772.28
COV			0.14			0.04	0.04
A-CLT3/671	34.53	17.26	10.99	300	19.75	39.95	23,607.46
A-CLT3/672	43.01	21.51	13.69	300	27.46	49.76	19,714.23
A-CLT3/673	64.38	32.19	20.49	300	33.30	74.47	25,407.31
Mean			15.06			54.73	22,909.67
COV			0.33			0.33	0.13
H-CLT3/511	8.49	4.25	2.06	115	23.67	32.28	9,880.50
H-CLT3/512	12.90	6.45	3.13	123	29.85	49.01	14,633.14
H-CLT3/513	8.22	4.11	1.99	126	25.09	31.26	10,521.41
H-CLT3/514	12.29	6.15	2.98	114	41.09	46.72	10,281.76
H-CLT3/515	7.79	3.90	1.89	122	20.42	29.61	11,349.16
Mean			2.41			37.78	11,333.19
COV			0.25			0.25	0.19
H-CLT3/671	27.76	13.88	8.84	114	45.15	80.28	21,828.40
H-CLT3/672	14.53	7.27	4.62	121.5	26.53	42.02	16,107.79
H-CLT3/673	18.00	9.00	5.73	121	31.56	52.07	18,642.13
H-CLT3/674	19.64	9.82	6.25	120	30.21	56.80	17,665.62
H-CLT3/675	15.40	7.70	4.90	122	33.54	44.54	11,290.50
Mean			6.07			55.14	17,106.88
COV			0.28			0.28	0.21

CLT: cross-laminated timber, MOR: modulus of rupture.

Download Excel Table

Table 3 provides an overview of the effects of adding thickness to the outermost layer or replacing the cross-layer wood species. All types of acacia CLT with three layers and hybrid CLT with three layers showed that increasing the layer thickness had a positive influence on the strength of the CLT panels. The mean MOE of A-CLT3/67 of 22,909.67 MPa with a COV of 13% is better than that of A-CLT3/51, whose mean MOE is 13,772.28 MPa with a COV of 4%, meaning that the addition of 8 mm to each outer layer can increase 39.88% of the MOE of the acacia CLT 3 layer. In the hybrid CLT type, the mean MOE of H-CLT3/67 is 17,106.88 MPa with a COV of 7% and H-CLT3/51 is 11,333.19 MPa with a COV of 23%, meaning that the panel in this type of CLT with a thickness of 67 mm has a 33.75% higher MOE value than the CLT panel with a thickness of 51 mm. It is generally known that engineered wood strength decreases as the wood size increases; however, acacia CLT and hybrid CLT show increased strength as the wood size increases. The increase in CLT thickness was not applied overall; instead, the thickness increased only in the outer layer. Owing to the out-of-plane bending, the stress is concentrated in the middle layer, allowing the strength to potentially increase despite an increase in thickness.

In the case of the cross-layer wood species, replacing the cross layer with a lower-quality timber species had a negative effect on the MOE value. The MOE of H-CLT3/67 was 25.32% lower than that of A-CLT/67 and H-CLT3/51 is 17.71% lower than that of A-CLT3/51. This study showed different failure modes in CLT panels according to the characteristics of each panel type. Fig. 4 illustrates the failure modes of the CLT-type composed of acacia, and Fig. 5 illustrates the failure mechanisms observed with respect to the different compositions of the middle layer made of mindi.

Fig. 4. Failure mode of the bending test for acacia CLT panel. (a) Side view A-CLT3/51, (b) bottom view A-CLT3/51, (c) side viewA-CLT3/67, (d) bottom viewA-CLT3/67. CLT: cross-laminated timber.

Download Original Figure

Fig. 5. Failure mode of the bending test for hybrid CLT panel. (a) Side view H-CLT3/51, (b) side view H-CLT3/67. CLT: cross-laminated timber.

Download Original Figure

In A-CLT3/51 and A-CLT3/67, the most common failure was tensile failure at the bottom layer, with marked tearing of the timber fibers (Fig. 4). However, some samples were also subjected to rolling shear failure, which occurred after fiber tearing at the edge of the bottom layer of the CLT panel. The rolling shear was characterized by a z-pattern in the middle layer; this failure mode was likely due to the load distribution around the annual ring. Layer 3 failed in the form of fiber rupture because the load distribution acting on the tension area was fully carried by the outermost layer. This type did not experience true delamination failure; delamination occurred after tensile failure in the bottom layer and then propagated to the interface area of the bottom and middle layers.

The H-CLT3/51 and H-CLT3/67 samples showed similar failure patterns, namely, rolling shear failure in the middle layer following the annual ring pattern that propagated at the interface layer, resulting in delamination. This type of CLT did not experience tensile failure, because its ability to resist bending forces was not comparable to that of the longitudinal layer. In addition, polyurethane adhesive (PUR) tends to penetrate through the tracheids in softwood, which causes adhesive penetration into the mindi timber as the cross layer is less optimal, making the adhesive area more susceptible to delamination when subjected to bending loads (Kim et al., 2024b). Song and Kim (2023) suggested that the gluing of mixed timber CLT involving softwood requires a longer pressing time for deeper adhesive penetration and better delamination performance.

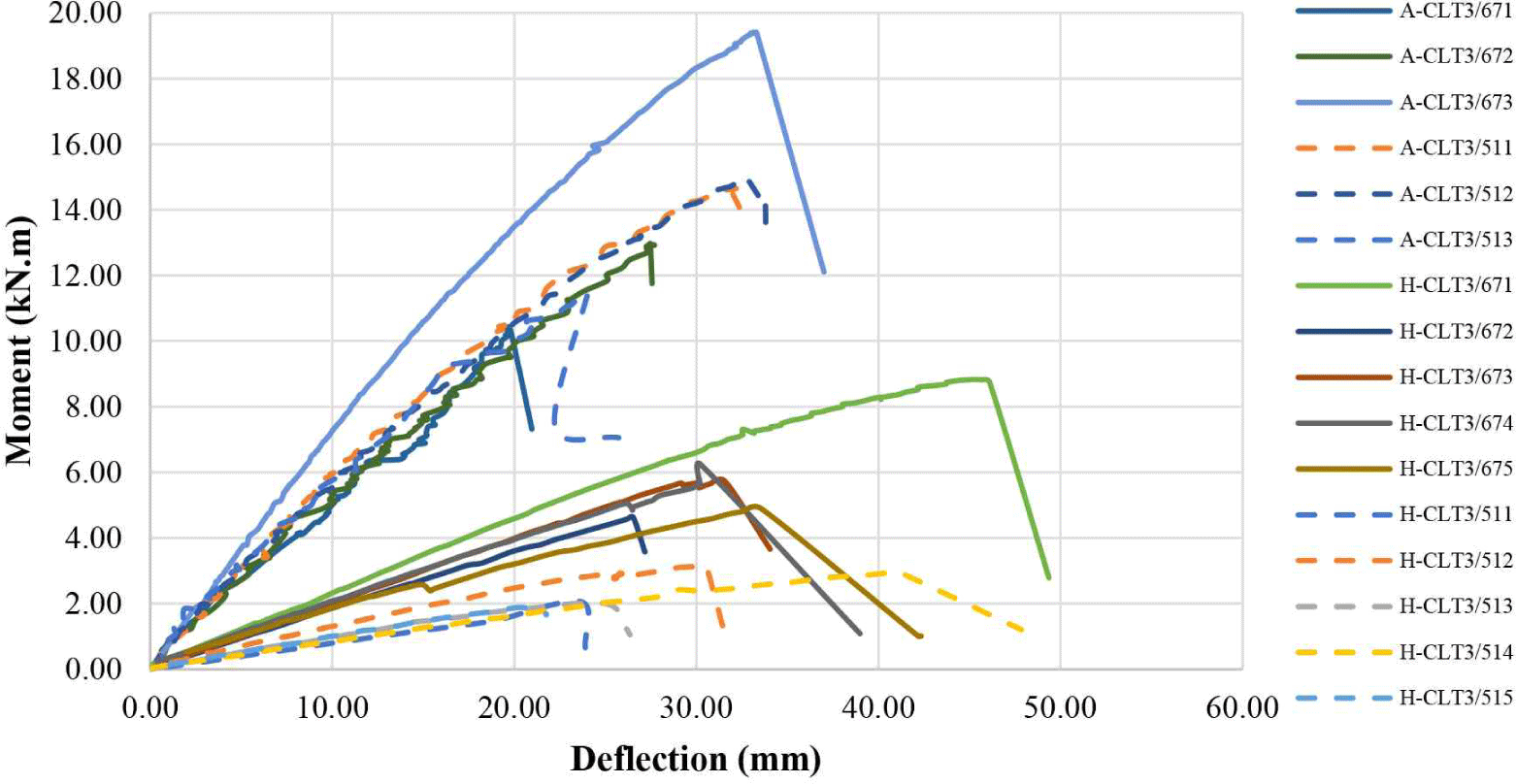
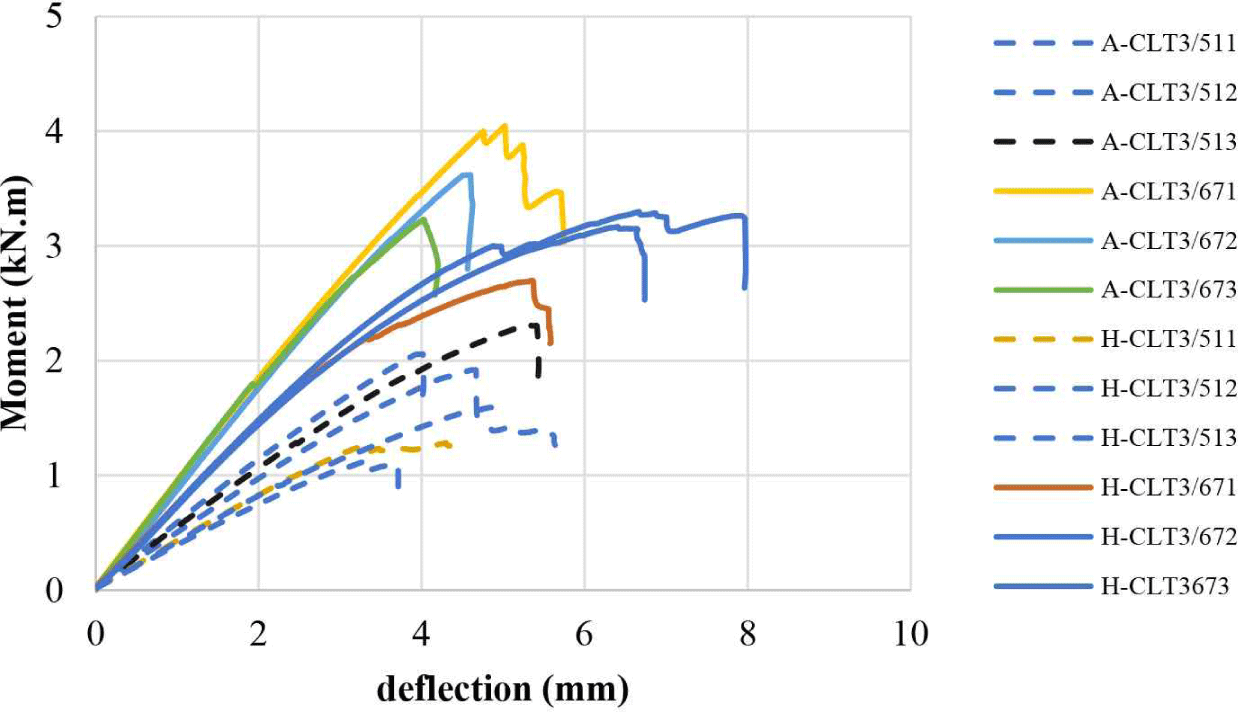
The moment-deflection correlation curves in Fig. 6 show the same pattern. The deflection was linear with the applied loading before reaching the maximum moment. A decrease occurred after the maximum moment was reached, and the CLT panel fractured. A-CLT3/51 reached an mean maximum moment of 10.46 kN.m with a COV of 14% while A-CLT3/67 reached a mean maximum moment of 15.06 kN.m with a COV of 33%. And in H-CLT3/51 and H-CLT3/67, the mean maximum moment were 2.41 kN.m (COV 25%) and 6.07 kN.m (COV 28%), respectively. From the moment versus deflection correlation curves, the initial stiffness of the acacia CLT was better than that of the hybrid CLT. This can be observed from the maximum deflection of the hybrid CLT being greater than that of the acacia CLT, and the degree of slope of the acacia CLT curve being greater than that of the hybrid CLT, as shown in Fig. 6.

Fig. 6. Moment-deflection curve of CLT bending specimen. CLT: cross-laminated timber.

Download Original Figure

The bending stiffness of the CLT sample was also calculated using the deflection measured during the test and then compared with the bending stiffness obtained using an analytical approach using several theories. A comparison between the test results and the theoretical calculations is presented in Table 4.

Table 4. Comparison of effective bending stiffness (EI) test and analytical approach

Sample code	Bending stiffness × 10¹⁰ (N.mm²)		Diff pred/test
Sample code	Bending stiffness × 10¹⁰ (N.mm²)		EI_gross		EI_Gamma		EI_SA		EI_Timoshenko
	EI∞	EIG	EI∞	EIG	EI∞	EIG	EI∞	EIG	EI∞	EIG
A-CLT3/511	4.49	4.68	0.89	0.85	0.86	0.86	0.87	0.84	0.83	0.80
A-CLT3/512	4.44	4.63	0.90	0.86	0.87	0.87	0.88	0.85	0.84	0.80
A-CLT3/513	4.77	5.00	0.83	0.80	0.81	0.81	0.82	0.78	0.78	0.75
Mean	4.57	4.77
COV	0.04	0.04
A-CLT3/671	17.75	18.35	0.51	0.49	0.50	0.50	0.50	0.49	0.47	0.46
A-CLT3/672	14.82	15.24	0.61	0.59	0.59	0.59	0.60	0.59	0.57	0.55
A-CLT3/673	19.10	19.80	0.47	0.46	0.46	0.46	0.47	0.45	0.44	0.43
Mean	17.23	17.80
COV	0.13	0.13
H-CLT3/511	1.26	1.29	1.27	1.23	1.15	1.15	1.18	1.15	1.25	1.22
H-CLT3/512	1.99	2.08	0.80	0.77	0.72	0.72	0.74	0.71	0.79	0.76
H-CLT3/513	1.47	1.51	1.09	1.05	0.98	0.98	1.01	0.98	1.07	1.04
H-CLT3/514	1.30	1.33	1.23	1.20	1.11	1.11	1.14	1.11	1.21	1.18
H-CLT3/515	1.53	1.58	1.04	1.01	0.94	0.94	0.97	0.94	1.03	1.00
Mean	1.51	1.56
COV	0.19	0.20
H-CLT3/671	6.24	6.48	0.58	0.56	0.53	0.51	0.54	0.52	0.58	0.56
H-CLT3/672	4.91	5.05	0.74	0.71	0.67	0.65	0.69	0.67	0.74	0.72
H-CLT3/673	5.65	5.85	0.64	0.62	0.58	0.56	0.59	0.57	0.64	0.62
H-CLT3/674	5.31	5.49	0.68	0.66	0.62	0.60	0.63	0.61	0.68	0.66
H-CLT3/675	3.45	3.52	1.05	1.02	0.96	0.94	0.98	0.96	1.05	1.03
Mean	5.11	5.28
COV	0.21	0.21

Download Excel Table

Based on the global stiffness calculation, it could be observed that A-CLT3/67 had an EI with an infinite shear modulus of 17.23E + 10 N.mm² or 73.48% stiffer than A-CLT3/51 which had a mean bending stiffness value of 4.57E + 10 N.mm². H-CLT3/67 obtained a mean EI with infinite shear modulus of 5.11E + 10 N.mm² and H-CLT3/51 1.15E + 10 N.mm², meaning that H-CLT3/67 had an EI value with an infinite shear modulus 70.45% higher than H-CLT3/51.

Sikora et al. (2016) reported that the thickness of a CLT panel was positively correlated with its stiffness. Overall, this study showed a uniform behavior in the correlation between the stiffness and panel thickness. However, in this study, the replacement of the cross layer with a lower-grade material reduced the stiffness by 66.95% %in CLT3/51 and 70.34% in CLT3/67.

The theoretical bending stiffnesses EI_gross, EI_gamma, EI_SA, EI_timoshenko resulted in similar values. EI_global was calculated using the deflection measured using the LVDT. Fig. 7 illustrated that EI_global with infinite shear modulus (EI_∞) showed lower values compared to EI_global calculated using a shear modulus (G), G or shear modulus was obtained using the approach recommended by the wood handbook (Gedeon, 2010) which recommends that the value of G = 1/20 of the value of E₀ for hardwood species. This means that the EI_global with an infinite shear modulus was closer to the theoretical EI than the EI with a given shear modulus. This was similar to the study conducted in, He et al. (2018) in which the EI value with an infinite shear modulus had a smaller difference than the theoretical calculation.

Fig. 7. Comparison experimental and theoretical bending stiffness CLT panel. (a) A-CLT3/51, (b) A-CLT3/67, (c) H-CLT3/51, (d) H-CLT3/67. CLT: cross-laminated timber.

Download Original Figure

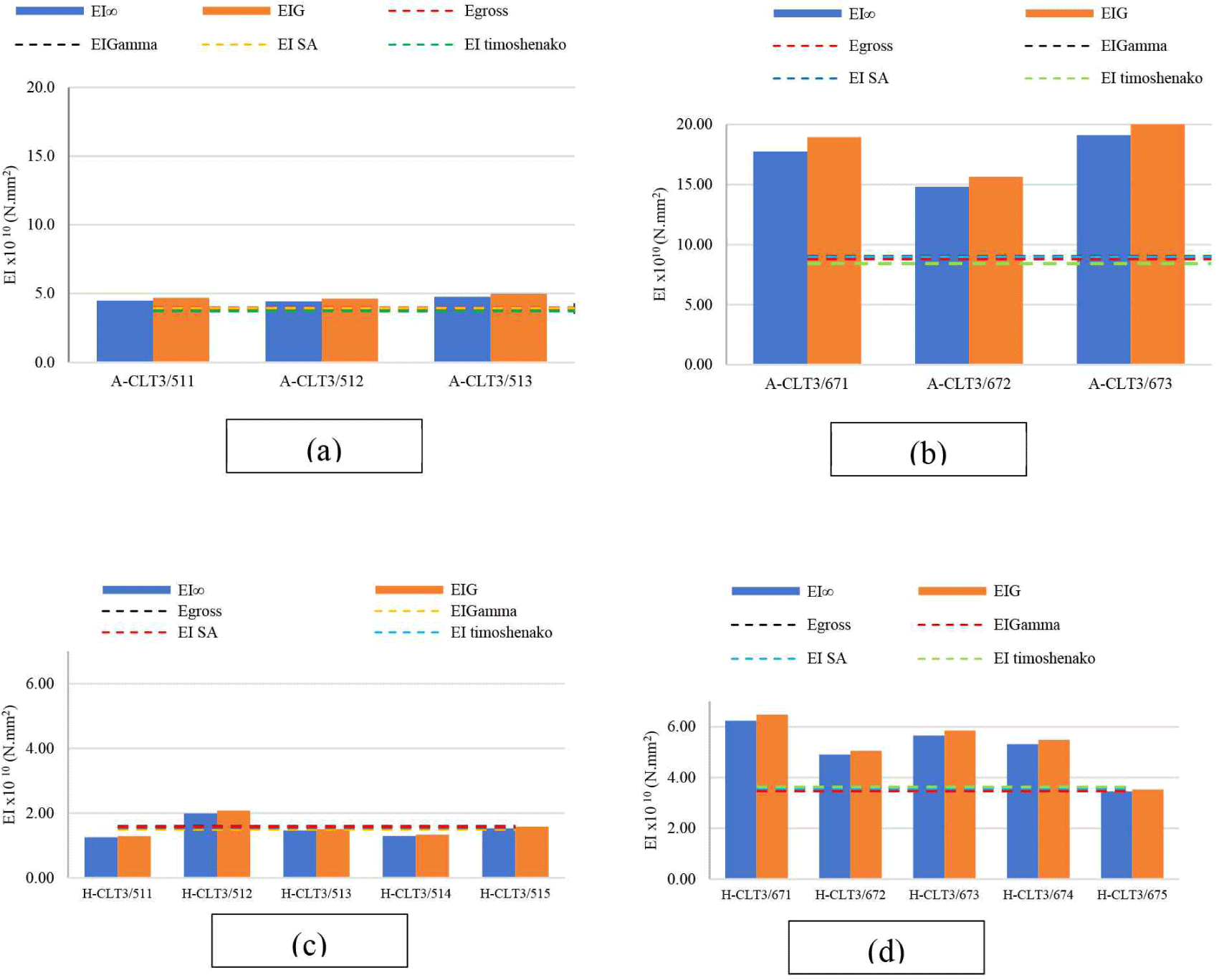
Fig. 7 and Table 4 illustrate the comparison of the EI test and prediction results, where the CLT panel type with a nonuniform layer thickness produced a much higher global EI than the EI predicted using several theories. It could be concluded that the characteristics of CLT composed of layers that have non-uniform thickness were different from CLT panels composed of layers with uniform thickness, from the equations offered in several theories had not been able to accommodate predictions on CLT panels with non-uniform layer thickness, especially using tropical hardwoods such as acacia timber and mindi timber as in this study.

3.2. Shear test

The results of the shear tests are summarized in Table 5. Maximum load (F_max); maximum shear capacity (V_max); maximum mid-span moment (M_max); and Δ_max is the deflection at ultimate load taken from measurements.

Table 5. Results obtained from shear bending tests

Sample type	F_max (kN)	V_max (kN)	M_max (kN.m)	Width (mm)	Δ_max (mm)	MOR (MPa)
A-CLT3/511	25.10	12.55	1.92	140.00	4.66	15.82
A-CLT3/512	26.89	13.44	2.06	140.00	4.02	16.95
A-CLT3/513	30.21	15.10	2.31	140.00	5.42	19.04
Mean	27.40		2.10
COV	0.09		0.09
A-CLT3/671	40.25	20.12	4.04	140.00	5.02	19.31
A-CLT3/672	36.00	18.00	3.62	140.00	4.60	17.27
A-CLT3/673	32.14	16.07	3.23	140.00	4.03	15.42
Mean	36.13		3.63
COV	0.11		0.11
H-CLT3/511	19.98	9.99	1.53	120.00	7.38	12.59
H-CLT3/512	15.07	7.54	1.15	120.00	3.33	9.30
H-CLT3/513	20.81	10.40	1.59	120.00	4.83	13.11
Mean	18.62		1.42
COV	0.17		0.17
H-CLT3/671	26.85	13.43	2.70	120.00	5.36	12.88
H-CLT3/672	31.50	15.75	3.17	120.00	6.41	15.11
H-CLT3/673	32.82	16.41	3.30	120.00	6.67	15.74
Mean	30.39		3.05
COV	0.10		0.10

MOR: modulus of rupture, CLT: cross-laminated timber.

Download Excel Table

The shear test results are shown in Table 5; a positive correlation was observed between the increase in layer thickness Vmax and MOR, with the increase being significant. A-CLT67 showed 33% higher Vmax than A-CLT51, whereas H-CLT67 produced 64% higher Vmax than H-CLT51. When compared with the composition of the constituent materials, the Vmax of A-CLT3/51 was 33% higher than that of H-CLT3/51, whereas that of A-CLT3/67 was 16% higher than that of H-CLT3/51. This meant that the thickness of layer and middle layer material affected the shear capacity, and MOR that can be carried by CLT panels. This result is in line with the report Li et al. (2021) that the shear capacity has a positive relationship with an increase in thickness; the thicker the CLT, the higher the shear capacity, and the shear strength of the CLT panel is influenced by the shear strength and fiber direction owing to the lamination of the transverse layer (Ma et al., 2021).

The moment and deflection correlation curve in Fig. 8 shows that at the same thickness of the CLT acacia panel, the linear area was longer than that of the hybrid CLT panel because each layer has the same characteristics, so that it holds the load more evenly and is more rigid than the hybrid CLT.

Fig. 8. Curve moment-deflection of shear specimen. CLT: cross-laminated timber.

Download Original Figure

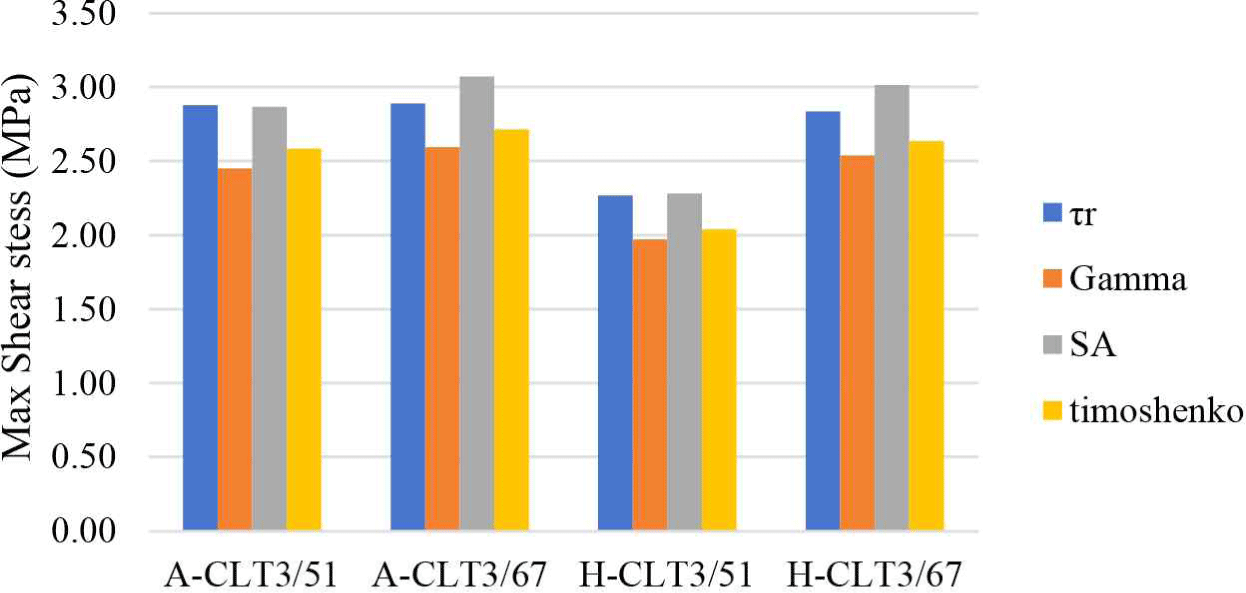
The failure modes of the CLT panels in the shear tests exhibited similar results. Acacia CLT exhibited an identical failure mode of rolling shear with a typical rolling shear failure mechanism in the middle layer. As shown in Fig. 9, the primary cracks in the transverse layer grew and spread along the annual ring orientation in the shear span before suddenly failing and dispersing in z- or multiple z-shaped patterns. The rolling shear failure pattern in the middle layer of the CLT is a common failure that occurs under high shear stress conditions (Kim et al., 2024a). Similar results were reported in Li (2017) an Li et al. (2021) examination of the CLT rolling shear strength characteristics of Radiata pine (Pinus radiata). Failure from the initial rolling shear close to the bond line was manifested as a shear stress transverse to the grain in the rolling shear behavior of the acacia CLT (Mohd Yusof et al., 2019). Notably, there was no evidence of adhesive failure (delamination) during the testing. The highest stiffness was observed in A-CLT3/67 panels, measured at 1.23E + 10 N.mm² with a COV of 0.03 using infinite shear modulus G and 1.53E + 10 N.mm² with a COV of 0.04 using shear modulus 1/20 E₀. The increase in thickness was found to be directly proportional to the stiffness. As shown in Table 6, for the same thickness, the stiffness of H-CLT3/67 was 19% lower than that of A-CLT3/67. This indicated that the stiffness of the CLT panel was affected by the replacement of the middle layer. Shear strength (τ_r) test and analytical approach summarized in Table 6.

Fig. 9. Shear test sample failure modes. (a) A-CLT3/51, (b) A-CLT3/67, (c) H-CLT3/51, (d) H-CLT3/67. CLT: cross-laminated timber.

Download Original Figure

Table 6. Comparison test results and analytical approach of shear stress

Kode	Bending stiffness × 10¹⁰ (N.mm²)		Shear stress (MPa)
Kode	EI∞	EI_G	τ _test	τ _Gamma	τ _SA	τ _timoshenko
A-CLT3/511	0.37	0.43	2.64	2.24	2.63	2.37
A-CLT3/512	0.44	0.53	2.82	2.40	2.81	2.53
A-CLT3/513	0.41	0.48	3.17	2.70	3.16	2.85
Mean			2.88
COV			0.09
A-CLT3/671	1.23	1.52	3.22	2.89	3.42	3.02
A-CLT3/672	1.19	1.47	2.88	2.58	3.06	2.70
A-CLT3/673	1.27	1.59	2.57	2.31	2.73	2.41
Mean	1.23	1.53	2.89
COV	0.03	0.04	0.11
H-CLT3/511	0.324	0.37	2.45	2.11	2.44	2.20
H-CLT3/512	0.294	0.33	1.85	1.60	1.84	1.63
H-CLT3/513	0.323	0.36	2.55	2.20	2.54	2.29
Mean			2.28
COV			0.17
H-CLT3/671	0.995	1.18	2.50	2.24	2.66	2.33
H-CLT3/672	0.996	1.18	2.94	2.63	3.13	2.73
H-CLT3/673	1.01	1.20	3.06	2.74	3.26	2.84
Mean			2.84
COV			0.10

CLT: cross-laminated timber.

Download Excel Table

In terms of shear stress in each sample, the best shear stress was in sample A-CLT3/67 with a value of τ_r 2.89 MPa (COV 0.11), 0.01 MPa higher than that of A-CLT3/51. The addition of outer layer dimension did not significantly affect the shear stress (τ_r) in A-CLT3, the increase was around 0.34% and in H-CLT3 the increase is 19.71%. Modification of the cross section using mindi wood decreased the shear stress by 26.31% in the 51 mm thick CLT and by 1.76% in the 67 mm thick CLT.

This is not in line with, Sikora et al. (2016) who mentioned that increasing the thickness of the CLT decreases the shear stress. In this case, if the thickness is added only to the outer layer, the maximum shear stress does not decrease. The determining factor for the shear stress of the CLT panels was the performance of the middle layer; however, the (Yang et al., 2021) strength distribution in the thicker outer layer caused the shear stress to increase, although it was not significant.

The test shear stress was calculated using Equation (4) assuming an isotropic material. The shear stress was calculated using several equations: gamma theory, SA, and Timoshenako. The results are illustrated in Fig. 10, which shows that the approach using SA was more conservative in predicting the relevant shear stress on the CLT panels investigated in this study.

Fig. 10. Comparison test results and analytical approach of shear stress. SA: shear analogy, CLT: cross-laminated timber.

Download Original Figure

3.3. Non-uniformity thickness layer effect

In this study, the thickness and bending stiffness had a positive correlation, meaning that the thicker the CLT panel, the greater the stiffness, which is in line with the research conducted by He et al. (2020) and Sikora et al. (2016). In this case, increasing the thickness of the outer layer with the load orientation on the major axis increased the bending stiffness of the CLT panel because the outer layer had the most significant influence on the bending strength of the CLT, was responsible for the bending load capacity, and tended to be zero in the middle layer (Hematabadi et al., 2021; Song and Kim, 2023). The replacement of the middle layer with a lower-quality material was recorded to reduce the bending stiffness of the CLT panel by more than 60% because the middle layer experienced shear failure before the failure of the outer layer. Therefore, the replacement of the middle layer with mindi in this case was deemed ineffective. The use of timber species of equal quality would have been more efficient in optimizing the performance of each layer according to its role.

In terms of the shear properties, the addition of an outer layer to all types of CLT resulted in a maximum shear stress increase of only 19%. This is because the outer layer, as the longitudinal layer of the CLT panel, experienced more residual stress from the middle layer, which caused a higher concentration of shear stress. Glasner et al. (2023) suggested that the thickness of the cross-layer is inversely proportional to the shear stress: the thicker the cross-layer, the smaller the shear stress, and the smaller the cross-layer thickness, the greater the shear stress. In fact, in this study, without changing the thickness of the cross layer, increasing the thickness of the outermost layer significantly increased the stiffness; an increase of 277% occurred in the CLT made of acacia wood, with an increase in shear stress of only 0.34%. A similar trend was observed for the hybrid CLT. Therefore, balancing the layer thickness to increase the stiffness without excessively increasing the shear stress is important in CLT panel designs.

4. CONCLUSIONS

Based on the investigations presented on the mechanical performance of CLTs made from acacia and acacia-mindi combined, it can be concluded that:

Acacia CLT had better stiffness than the hybrid CLT because, in acacia CLT panels, the lamina as a whole worked optimally according to the expected mechanism, whereas in the hybrid CLT, the lamina in the tensile and compressive areas did not work optimally in resisting stress due to major direction loading. The cross layer failed first in the form of a shear failure following the annual ring. Therefore, an equivalent timber must be selected so that the CLT panel can operate optimally.
An increase in the outer layer thickness effectively enhanced the stiffness by 277% in acacia CLT and 238.41% in hybrid CLT. Conversely, positioning mindi wood as the cross-layer in the hybrid CLT reduced the bending stiffness by 66.95% in the CLT with a thickness of 51 mm and by 70.34% in the CLT with a thickness of 67 mm.
The effect of the outer layer modification on the shear stress was not significant in acacia CLT, as it only decreased by 0.34%. In the hybrid CLT, the shear stress declined by 19.71%. Compared to each constituent material composition, a reduction of 26.31% occurred in the CLT with a thickness of 51 mm and 1.76% in the CLT with a thickness of 67 mm.
A theoretical SA approach can be used to predict the stiffness and shear stress of CLT panels composed of laminae of uniform thickness. For CLT panels with non-uniform lamina thickness, another mathematical approach is required to predict their performance more precisely.

CONFLICT of INTEREST

No potential conflict of interest relevant to this article was reported.

ACKNOWLEDGMENT

The authors gratefully acknowledge the generous support provided by InCLT for providing all samples used in our study. This research was financially supported by a doctoral disk research grant (UNS) with contract research: 194.2/UN27.22/PT.01.03/2024.

REFERENCES

American Society for Testing and Materials [ASTM]. 2014. Standard Test Methods for Small Clear Specimens of Timber. ASTM D143-14. ASTM International, West Conshohocken, PA, USA.

American Society for Testing and Materials [ASTM]. 2015. Standard Test Methods of Static Tests of Lumber in Structural Sizes. ASTM D198-15. ASTM International, West Conshohocken, PA, USA.

Brandner, R., Flatscher, G., Ringhofer, A., Schickhofer, G., Thiel, A. 2016. Cross laminated timber (CLT): Overview and development. European Journal of Wood and Wood Products 74(3): 331-351.

Christovasilis, I.P., Brunetti, M., Follesa, M., Nocetti, M., Vassallo, D. 2016. Evaluation of the mechanical properties of cross laminated timber with elementary beam theories. Construction and Building Materials 122: 202-213.

Crovella, P., Smith, W., Bartczak, J. 2019. Experimental verification of shear analogy approach to predict bending stiffness for softwood and hardwood cross-laminated timber panels. Construction and Building Materials 229: 116895.

Ehrhart, T., Brandner, R. 2018. Rolling shear: Test configurations and properties of some European soft- and hardwood species. Engineering Structures 172: 554-572.

Galih, N.M., Yang, S.M., Yu, S.M., Kang, S.G. 2020. Study on the mechanical properties of tropical hybrid cross laminated timber using bamboo laminated board as core layer. Journal of the Korean Wood Science and Technology 48(2): 245-252.

Gedeon, G. 2010. Wood Handbook: Wood as an Engineering Material. US Forest Service, Washington, DC, USA.

Glasner, D., Ringhofer, A., Brandner, R., Schickhofer, G. 2023. Rolling shear strength of cross laminated timber (CLT): Testing, evaluation, and design. Buildings 13(11): 2831.

10.

Hariz, T.M.R., Hadi, Y.S., Lubis, M.A.R., Maulana, M.I., Sari, R.K., Hidayat, W. 2023. Physical and mechanical properties of cross-laminated timber made of a combination of Mangium-Puspa wood and polyurethane adhesive. Jurnal Sylva Lestari 11(1): 37-65.

11.

He, M., Sun, X., Li, Z. 2018. Bending and compressive properties of cross-laminated timber (CLT) panels made from Canadian hemlock. Construction and Building Materials 185: 175-183.

12.

He, M., Sun, X., Li, Z., Feng, W. 2020. Bending, shear, and compressive properties of three- and five-layer cross-laminated timber fabricated with black spruce. Journal of Wood Science 66: 38.

13.

Hematabadi, H., Madhoushi, M., Khazaeian, A., Ebrahimi, G. 2021. Structural performance of hybrid poplar-beech cross-laminated-timber (CLT). Journal of Building Engineering 44: 102959.

14.

Hematabadi, H., Madhoushi, M., Khazaeyan, A., Ebrahimi, G., Hindman, D., Loferski, J. 2020. Bending and shear properties of cross-laminated timber panels made of poplar (Populus alba). Construction and Building Materials 265: 120326.

15.

Hindman, D.P., Bouldin, J.C. 2015. Mechanical properties of southern pine cross-laminated timber. Journal of Materials in Civil Engineering 27(9): 04014251.

16.

Huang, Z., Huang, D., Chui, Y.H., Chen, Z. 2023a. A layered beam-based model for analyzing the stress of rolling shear for the cross-laminated timber panels under out-of-plane bending. Engineering Structures 289: 116290.

17.

Huang, Z., Jiang, L., Ni, C., Chen, Z. 2023b. The appropriacy of the analytical models for calculating the shear capacity of cross-laminated timber (CLT) under out-of-plane bending. Journal of Wood Science 69(1): 14.

18.

Karacabeyli, E., Gagnon, S. 2019. Canadian CLT Handbook, 2019 Edition (QC). National Library of Canada, Ottawa, ON, Canada.

19.

Kim, J., Ahn, K.S., Pang, S.J., Song, D., Kim, C.K., Kim, K., Shim, K., Kim, K.H., Oh, J.K. 2024a. Effective measuring area and test protocol in picture frame method to measure in-plane shear modulus of cross-laminated timber. Journal of the Korean Wood Science and Technology 52(6): 605-617.

20.

Kim, K.H., Lee, H.M., Lee, M. 2024b. Erratum to: Evaluation of adhesive characteristics of mixed cross laminated timber (CLT) using yellow poplar and softwood structural lumber. Journal of the Korean Wood Science and Technology 52(4): 404.

21.

Li, M. 2017. Evaluating rolling shear strength properties of cross-laminated timber by short-span bending tests and modified planar shear tests. Journal of Wood Science 63(4): 331-337.

22.

Li, X., Ashraf, M., Subhani, M., Kremer, P., Kafle, B., Ghabraie, K. 2020. Experimental and numerical study on bending properties of heterogeneous lamella layups in cross laminated timber using Australian Radiata pine. Construction and Building Materials 247: 118525.

23.

Li, X., Ashraf, M., Subhani, M., Kremer, P., Li, H., Anwar-Us-Saadat, M. 2021. Rolling shear properties of cross-laminated timber (CLT) made from Australian Radiata pine: An experimental study. Structures 33: 423-432.

24.

Ma, Y., Si, R., Musah, M., Dai, Q., Xie, X., Wang, X., Ross, R.J. 2021. Mechanical property evaluation of hybrid mixed-species CLT panels with sugar maple and white spruce. Journal of Materials in Civil Engineering 33(7): 04021171.

25.

Mohd Yusof, N., Md Tahir, P., Lee, S.H., Khan, M.A., Mohammad Suffian James, R. 2019. Mechanical and physical properties of cross-laminated timber made from Acacia mangium wood as function of adhesive types. Journal of Wood Science 65: 20.

26.

Navaratnam, S., Christopher, P.B., Ngo, T., Le, T.V. 2020. Bending and shear performance of Australian Radiata pine cross-laminated timber. Construction and Building Materials 232: 117215.

27.

Rahman, M.D.T., Ashraf, M., Ghabraie, K., Subhani, M. 2020. Evaluating timoshenko method for analyzing CLT under out-of-plane loading. Buildings 10(10): 1-21.

28.

Sikora, K.S., McPolin, D.O., Harte, A.M. 2016. Effects of the thickness of cross-laminated timber (CLT) panels made from Irish Sitka spruce on mechanical performance in bending and shear. Construction and Building Materials 116: 141-150.

29.

Song, D.B., Kim, K.H. 2023. Influence of composition of layer layout on bending and compression strength performance of larix cross-laminated timber (CLT). Journal of the Korean Wood Science and Technology 51(4): 239-252.

30.

Trisatya, D.R., Santoso, A., Abdurrachman, A., Prastiwi, D.A. 2023. Performance of six-layered cross laminated timber of fast-growing species glued with tannin resorcinol formaldehyde. Journal of the Korean Wood Science and Technology 51(2): 81-97.

31.

Ukyo, S., Miyatake, A., Shindo, K., Hiramatsu, Y. 2021. Shear strength properties of hybrid (hinoki cypress and Japanese cedar) cross-laminated timber. Journal of Wood Science 67: 23.

32.

Wallner-Novak, M., Koppelhuber, J., Pock, K. 2014. Cross-Laminated Timber Structural Design: Basic Design and Engineering Principles according to Eurocode. ProHolz, Salzburg, Austria.

33.

Yang, S.M., Lee, H.H., Kang, S.G. 2021. Research trends in hybrid cross-laminated timber (CLT) to enhance the rolling shear strength of CLT. Journal of the Korean Wood Science and Technology 49(4): 336-359.